Asymptoten der Hyperbel

Gegeben sei eine Hyperbel in Mittelpunktslage, d.h. eine Hyperbel mit folgender Gleichung:
$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$

Auflösen dieser Gleichung nach y ergibt:
$y=\pm \frac{b}{a}x\sqrt{1-\frac{a^2}{x^2}}$

Für $x\to \pm \infty$ strebt der Ausdruck $\frac{a^2}{x^2}$ gegen null und damit ergeben sich als Gleichungen der Asymptoten:
$y=\pm \frac{b}{a}x$

• Beispiel 1: Es sind die Asymptoten der Hyperbel mit der Gleichung
  $\frac{x^2}{4}-\frac{y^2}{9}=1$ zu bestimmen.
  
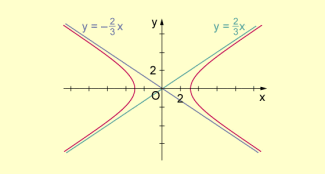
  Wegen $a=3undb=2$ erhält man die in der folgenden Abbildung angegebenen Asymptoten.

Analog lassen sich die Gleichungen der Asymptoten für eine Hyperbel in allgemeiner (achsenparalleler) Lage, d.h. eine Hyperbel mit der Gleichung
$\frac{{\left(x-c\right)}^2}{a^2}-\frac{{\left(y-d\right)}^2}{b^2}=1$, bestimmen.

Für den Anstieg der Asymptoten gilt auch hier $m=\pm \frac{b}{a}$, und sie gehen durch den Punkt M(c; d).

• Beispiel 2: Es sind die Asymptoten der Hyperbel mit der Gleichung
  $\frac{{\left(x-2\right)}^2}{16}-\frac{{\left(y+3\right)}^2}{8}=1$ zu bestimmen.
  
  Für den Anstieg gilt $m=\pm \frac{4}{\sqrt{8}}=\pm \frac{4}{2\sqrt{2}}=\pm \frac{2}{\sqrt{2}}=\pm \sqrt{2}.$
  Einsetzen in die Punktrichtungsgleichung ergibt $y+3=\pm \sqrt{2}\left(x-2\right).$
  
  Somit lauten die Gleichungen der Asymptoten in expliziter Form:
  $\begin{array}{c}y=f_1\left(x\right)=\sqrt{2}x-\left(2\sqrt{2}+3\right)\\ y=f_2\left(x\right)=-\sqrt{2}x+\left(2\sqrt{2}-3\right)=-\sqrt{2}x-\left(3-2\sqrt{2}\right)\end{array}$