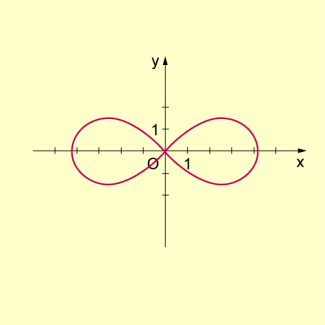Kurven in Polarkoordinatendarstellung

Kegelschnitte

Zur Darstellung von Kegelschnitten in Polarkoordinaten werden die Formeln für die Umrechnung von kartesischen Koordinaten in Polarkoordinaten $x=r\cos \varphi$ und $y=r\sin \varphi$ in die Scheitel- bzw. Mittelpunktsgleichungen eingesetzt und diese umgeformt.

Als Beispiel dafür betrachten wir im Folgenden die Parabel mit dem Brennpunkt im Koordinatenursprung mit der folgenden Scheitelgleichung:
$y^2=2p\left(x+\frac{p}{2}\right)S\left(-\frac{p}{2};0\right)$

Einsetzen der oben angegebenen Formeln für die Umrechung ergibt:
${\left(r\sin \varphi \right)}^2=2p\left(r\cos \varphi +\frac{p}{2}\right)$

Daraus folgt für $0°\le \varphi <360°$ die Polargleichung einer Parabel:
$r=\frac{p}{1-\cos \varphi }$

Auch hier gilt die Verallgemeinerung für alle Kegelschnitte, und es ist:
$r=\frac{p}{1-\epsilon \cos \varphi }$

Für $\epsilon =0$ handelt es sich um einen Kreis, für $0<\epsilon <1$ um eine Ellipse, für $\epsilon =1$ um eine Parabel und für $1<\epsilon$ um eine Hyperbel.

Spiralen

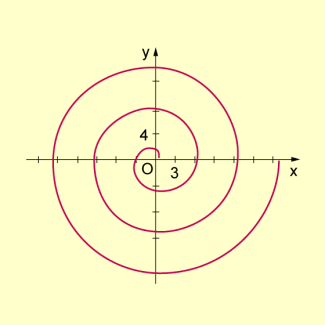
1. Archimedische Spirale

Ein Strahl $\overline{OP}$ dreht sich mit konstanter Geschwindigkeit um P und bewegt sich gleichzeitig gleichförmig von O weg (z.B. die Laufkatze eines Drehkranes). Die Länge des Strahles $\overline{OP}$ ändert sich proportional mit dem Drehwinkel.

Die Gleichung für die archimedische Spirale in Polarkoordinaten lautet:
$r=a\varphi$

Parameterdarstellung:
$\begin{array}{l}x=a\varphi \cos \varphi \\ y=a\varphi \sin \varphi \left(a>0;\varphi \ge 0\right) \end{array}$

Die folgende Abbildung zeigen die Kurve für $a=1$ und $0\le \varphi <6\pi$.

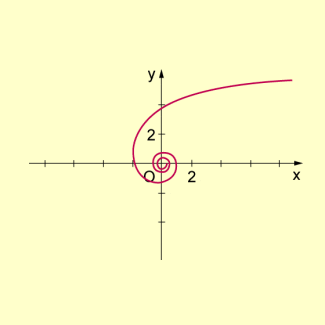
2. Hyperbolische Spirale

Bei dieser Spirale ist die Länge des Strahles $\overline{OP}$ umgekehrt proportional zum Drehwinkel. Die Gleichung für die hyperbolische Spirale in Polarkoordinaten lautet:
$r=\frac{a}{\varphi }$

Wegen $\underset{\varphi \to \infty }{\lim }r=0$ nähert sich die Spirale asymptotisch dem Ursprung.
Parameterdarstellung:
$\begin{array}{l}x=\frac{1}{a\varphi }\cos \varphi \\ y=\frac{1}{a\varphi }\sin \varphi \left(a>0;\varphi >0\right)\end{array}$

In der folgenden Abbildung ist die hyperbolische Spirale für $a=6$ und $\mathrm{0,5}<\varphi \le 6\pi$ dargestellt.

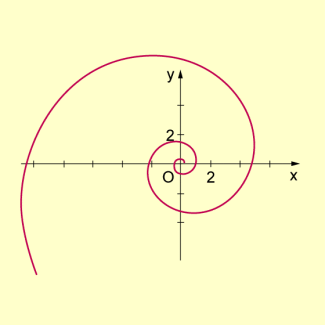
3. Logarithmische Spirale

Die logarithmische Spirale wird durch die Polargleichung $r=e^{a\varphi }$ beschrieben.
Für $\varphi \to -\infty$ nähert sich die Spirale beliebig dem Ursprung und für $\varphi \to \infty$ geht auch $r\to \infty .$

Parameterdarstellung:
$\begin{array}{l}x=e^{a\varphi }\cos \varphi \\ y=e^{a\varphi }\sin \varphi \left(\varphi \in ℝ\right)\end{array}$

In der folgenden Abbildung ist die Kurve für $a=\frac{1}{4}$ und $-2\pi \le \varphi <10$ dargestellt.

Schraubenkurve

Auf der Oberfläche eines rotierenden geraden Kreiszylinders bewegt sich ein Punkt mit konstanter Geschwindigkeit in z-Richtung:
$\begin{array}{l}\lambda =\arctan \frac{c\varphi }{r}\\ \rho =\overline{OP}=\sqrt{r^2+c^2{\varphi }^2}\end{array}$

Cassinische Kurven

Cassinische Kurven (benannt nach GIOVANNI DOMENICO CASSINI, 1625 bis 1712) sind definiert als der geometrische Ort aller Punkte P, für die das Produkt der Abstände der Brennpunkte $F_{1}und{F}_2$ vom Mittelpunkt M einen konstanten Wert $a^2$ besitzt. Der Abstand von $F_{1}und{F}_2$ sei 2c. Das Verhältnis von a und c ist für die Gestalt der Kurve von Bedeutung.

Die Polarkoordinatendarstellung für cassinische Kurven lautet:
$r=\sqrt{c^2\cos 2\varphi \pm \sqrt{c^4{\cos }^{2}2\varphi +a^4{c}^4}}$

Die folgende Abbildung zeigt die Kurve für $a=1undc=3$.

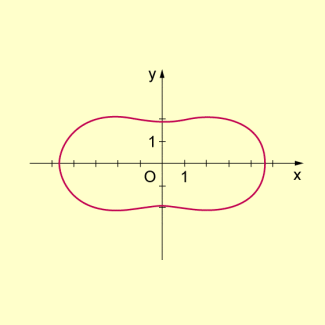
Für die Lemniskate als Spezialfall der cassinischen Kurven erhält man für $a^2=c^2$ die Gleichung $r=a\sqrt{2\cos 2\varphi }.$

In der folgenden Abbildung ist die Kurve für $a=3$ dargestellt.