Koordinatentransformationen

Parallelverschiebung eines Koordinatensystems

Als Erstes soll eine Parallelverschiebung (Translation) eines räumlichen Koordinatensystems betrachtet werden.

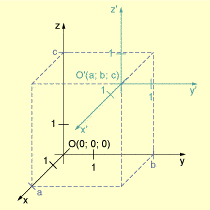
Der Ursprung des neuen Koordinatensystems sei $O\text{'}\left(a;b;c\right)$. Zwischen den Koordinaten x, y und z eines Punktes P im gegebenen Koordinatensystem und seinen Koordinaten $x\text{'},y\text{'},z\text{'}$ im neuen System besteht dann der folgende Zusammenhang:
$\begin{array}{ccc}x\text{'}=x-a& bzw.& x=x\text{'}+a\\ y\text{'}=y-b& & y=y\text{'}+b\\ z\text{'}=z-c& & z=z\text{'}+c\end{array}$

Im Folgenden soll ein Beispiel für die Ebene betrachtet werden.

• Beispiel: Gegeben sei eine kubische Parabel durch $y=f\left(x\right)=\frac{1}{10}{x}^3-\frac{3}{10}{x}^2-\frac{3}{5}x+\frac{9}{5}$.
  Wie ändert sich deren Gleichung, wenn eine Verschiebung des Koordinatenursprungs in den Punkt $O\text{'}\left(1;1\right)$ vorgenommen wird?

Mithilfe der Beziehungen $x=x\text{'}+1bzw.y=y\text{'}+1$ ergibt sich:
$\begin{array}{c} y\text{'}=\frac{1}{10}{\left(x\text{'}+1\right)}^3-\frac{3}{10}{\left(x\text{'}+1\right)}^2-\frac{3}{5}\left(x\text{'}+1\right)+\frac{9}{5}\\ =\frac{1}{10}{\left(x\text{'}\right)}^3+\frac{3}{10}{\left(x\text{'}\right)}^2+\frac{3}{10}x\text{'}+\frac{1}{10}-\frac{3}{10}{\left(x\text{'}\right)}^2-\frac{6}{10}x\text{'}-\frac{3}{10}-\frac{3}{5}x\text{'}-\frac{3}{5}+\frac{9}{5}\\ =\frac{1}{10}{\left(x\text{'}\right)}^3-\frac{9}{10}x\text{'}\end{array}$

Aus dieser Darstellung kann z.B. die Punktsymmetrie des Graphen zum Ursprung $O\text{'}$ bzw. zum Punkt $P\left(1;1\right)$ im ursprünglichen Koordinatensystem sofort erkannt werden, da kein Absolutglied und kein Ausdruck mit geradzahligem Exponenten vorhanden ist.

Drehung eines Koordinatensystems um den Koordinatenursprung

Im Folgenden wird die Drehung (Rotation) eines ebenen Koordinatensystems betrachtet. Wird der Ursprung des Koordinatensystems beibehalten, d.h. gilt $O\text{'}=O$, und werden nur die Achsen um den Winkel $\varphi$ gedreht, dann ergeben sich folgende Transformationsgleichungen:
$\begin{array}{lll}x=x\text{'}\cdot \cos \varphi -y\text{'}\cdot \sin \varphi \hfill & bzw.\hfill & x\text{'}=x\cdot \cos \varphi +y\cdot \sin \varphi \hfill \\ y=x\text{'}\cdot \sin \varphi +y\text{'}\cdot \cos \varphi \hfill & \hfill & y\text{'}=-x\cdot \sin \varphi +y\cdot \cos \varphi \hfill \end{array}$

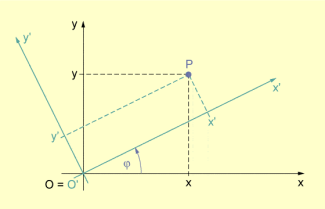
• Beispiel: Gegeben sei der Punkt $P\left(3;2\right)$. Das Koordinatensystem wird um $30°$ im mathematisch positiven Drehsinn gedreht.

Die neuen Koordinaten ergeben sich wie folgt:
$x\text{'}=3\cdot \cos 30°+2\cdot \sin 30°\approx \mathrm{3,598}$
$y\text{'}=-3\cdot \sin 30°+2\cdot \cos 30°\approx \mathrm{0,232}$

Analoge Überlegungen lassen sich für den dreidimensionalen Fall anstellen.