Darstellung von Vektoren
Unter einem Vektor versteht man die Menge aller Pfeile, die gleich lang, zueinander parallel und gleich orientiert sind.
Ein einzelner Pfeil aus dieser Menge heißt ein Repräsentant des Vektors.
Aus dieser Begriffsfestlegung ergibt sich die Möglichkeit, Vektoren in der Ebene und im Raum durch gerichtete Strecken darzustellen.
Fasst man Vektoren (allgemeiner) als n-Tupel reeller Zahlen auf, so führt dies zu einer Darstellung in Form einspaltiger bzw. einzeiliger Matrizen (Spalten- bzw. Zeilenvektoren).
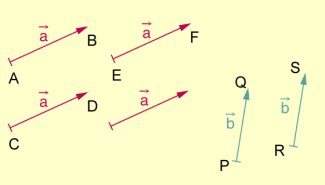
Beispielsweise lassen sich zwei Vektoren mit in der in der folgenden Abbildung angegebenen Weise darstellen.
-
Vektoren als gerichtete Strecken
Neben dieser aus der Anschauung sowie vor allem aus physikalischen Sachverhalten gewonnenen Auffassung des Begriffs Vektor steht die abstraktere algebraische Erklärung des Vektorbegriffs als n-Tupel reeller Zahlen.
Davon ausgehend wird dann ein Vektor als eine spezielle Matrix, nämlich als eine einspaltige Matrix (oder Spaltenvektor) bzw. eine einzeilige Matrix (oder Zeilenvektor) in folgender Form geschrieben:
Anmerkung:
Für die schreibtechnisch günstigere Darstellung eines Spaltenvektors
als Zeilenvektor (transponierter Spaltenvektor) wird mitunter auch die Schreibweise genutzt.
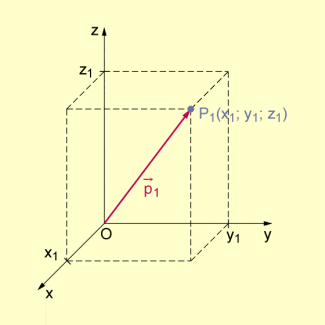
Im (räumlichen) kartesischen Koordinatensystem dient der Vektor in der Form des Ortsvektors auch zur Beschreibung der Lage von Punkten.
Der zum Punkt gehörende Ortsvektor würde dann folgendermaßen geschrieben:
-
Ortsvektor eines Punktes (im räumlichen kartesischen Koordinatensystem)