Skalarprodukt zweier Vektoren

Beispiel 1: Hebt man einen Gegenstand mit der Gewichtskraft $F_G$ z. B. vom Fußboden auf einen Tisch, so wird mechanische Arbeit verrichtet.
Diese Arbeit berechnet sich nach der bekannten Formel $W=F_s\cdot s$, wobei $F_s=\left|{\overrightarrow{F}}_s\right|$ der Betrag der vektoriellen Größe Kraft ist, die in Richtung des Weges $\overrightarrow{s}$ wirkt, und $s=\left|\overrightarrow{s}\right|$ die Länge dieses Weges angibt.
Im vorliegenden Fall haben ${\overrightarrow{F}}_s$ und $\overrightarrow{s}$ dieselbe Richtung.
Im Gegensatz zu den vektoriellen Größen Kraft und Weg lässt sich der mechanischen Arbeit keine Richtung zuordnen – es handelt sich hier um eine skalare Größe.

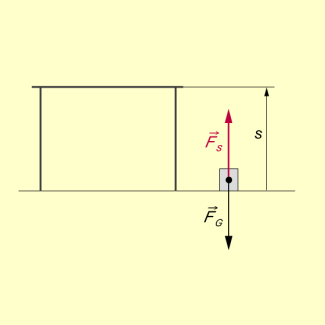
Beispiel 2: Wird nun ein Eisenbahnwagen auf Schienen von einem Traktor gezogen, der nicht auf diesen Schienen fährt, so wirkt auf den Wagen eine Kraft ${\overrightarrow{F}}_T$ in Richtung des Seiles, also im Unterschied zu obigem Beispiel nicht in Wegrichtung.
Dennoch kann man auch hier die mechanische Arbeit nach der Formel $W=F_s\cdot s$ berechnen, wenn man unter $F_s$ die Größe der Kraftkomponente versteht, die in Richtung des Weges wirkt.

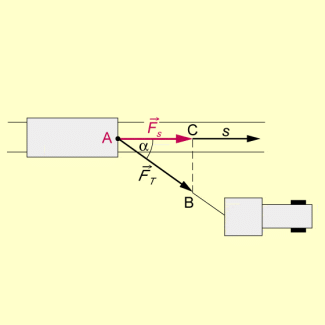
Ist $\alpha$ der Winkel zwischen den Kräften ${\overrightarrow{F}}_T$ und $F_s$, so gilt nach trigonometrischen Beziehungen im rechtwinkligen Dreieck ABC für die Größen dieser Kräfte $\left|{\overrightarrow{F}}_s\right|=\left|{\overrightarrow{F}}_T\right|\cdot \cos \alpha$.
Für die mechanische Arbeit erhalten wir also insgesamt $W=\left|{\overrightarrow{F}}_T\right|\cdot \left|\overrightarrow{s}\right|\cos \alpha$.
(Diese Formel gilt auch für das obige Beispiel, da dort $\alpha$ = 0° und damit cos $\alpha$ = 1 ist.)

Auf der linken Seite der obigen Gleichung steht mit W eine skalare, also nichtgerichtete Größe und auf der rechten Seite das Produkt aus den Beträgen zweier gerichteter Größen und dem Kosinus des eingeschlossenen Winkels. Ausgehend davon definieren wir nun ein Produkt zweier Vektoren. Weil das Resultat dieses Produktes ein Skalar, also eine reelle Zahl ist, heißt dieses Produkt Skalarprodukt.

• Definition: Sind $\overrightarrow{a}und\overrightarrow{b}$ zwei Vektoren, so nennt man $\overrightarrow{a}\cdot \overrightarrow{b}=\left|\overrightarrow{a}\right|\cdot \left|\overrightarrow{b}\right|\cdot \cos \alpha$ das Skalarprodukt der Vektoren $\overrightarrow{a}und\overrightarrow{b}$, wobei $\alpha$ den von $\overrightarrow{a}und\overrightarrow{b}$ eingeschlossenen Winkel bezeichnet.

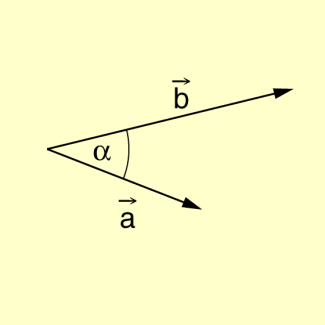
Das Skalarprodukt ist eine Rechenoperation in der Menge der Vektoren, die zwei Vektoren eine reelle Zahl zuordnet und damit aus dem Bereich der Vektoren herausführt.

Speziell gilt $\overrightarrow{a}\cdot \overrightarrow{b}=0$, wenn $\overrightarrow{a}=\overrightarrow{o}oder\overrightarrow{b}=\overrightarrow{o}$.
Das Skalarprodukt zweier Vektoren kann aber auch den Wert 0 annehmen, wenn beide Vektoren vom Nullvektor verschieden sind – nämlich dann, wenn die beiden Vektoren $\overrightarrow{a}und\overrightarrow{b}$ den Winkel 90° einschließen.

Einen Überblick über das Skalarprodukt bei allen Lagemöglichkeiten von $\overrightarrow{a}und\overrightarrow{b}$ gibt folgende Tabelle: