Betrag eines Vektors

Unter einem Vektor versteht man die Menge aller Pfeile, die gleich lang, zueinander parallel und gleich orientiert sind. Diese übereinstimmende Länge aller repräsentierenden Pfeile eines bestimmten Vektors nennt man dessen Betrag.

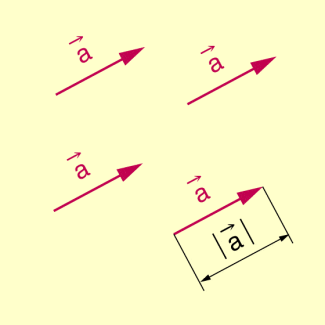
Der Betrag $| \vec{a} |$ eines Vektors $\vec{a}$ ist gleich der Länge der Strecke $\bar{A B}$ für einen beliebigen Repräsentanten $\vec{A B}$ von $\vec{a}$ . Gilt also $\vec{a} = \vec{A B}$ , so ist $| \vec{a} | = | \vec{A B} | .$
Im Spezialfall $| \vec{a} | = 1$ nennt man $\vec{a}$ einen Einheitsvektor.

Wird ein Vektor durch einen Pfeil mit den Endpunkten $P_{1} (x_{1}; y_{1})$ und $P_{2} (x_{2}; y_{2})$ in der Ebene bzw. $P_{1} (x_{1}; y_{1}; z_{1})$ und $P_{2} (x_{2}; y_{2}; z_{2})$ im Raum beschrieben, so lässt sich sein Betrag mithilfe des Satzes des PYTHAGORAS aus seinen Koordinaten berechnen.

Berechnung des Betrags eines Vektors

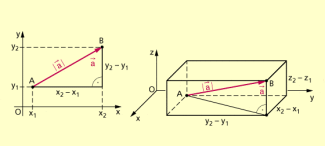
Es gilt dann:
$\begin{array}{l} | \vec{a} | = \sqrt{{(x_{2} - x_{1})}^{2} + {(y_{2} - y_{1})}^{2}} b z w . \\ | \vec{a} | = \sqrt{{(x_{2} - x_{1})}^{2} + {(y_{2} - y_{1})}^{2} + {(z_{2} - z_{1})}^{2}} \end{array}$

Beispiel 1: Ein Vektor $\vec{a}$ werde durch ein Pfeil mit den Endpunkten $P_{1} (3; 6; - 2) u n d P_{2} (- 8; 4; - 6)$ beschrieben.

Dann gilt:
$\begin{matrix} | \vec{a} | = \sqrt{{(- 8 - 3)}^{2} + {(4 - 6)}^{2} + {(- 6 - (- 2))}^{2}} \\ = \sqrt{121 + 4 + 16} = \sqrt{141} \end{matrix}$

Aus der Definition des Betrages eines Vektors als Streckenlänge sowie der Ungleichung für die Seitenlängen eines Dreiecks ergeben sich weiter folgende Regeln für das Rechnen mit den Beträgen beliebiger Vektoren $\vec{a} u n d \vec{b} :$
$\begin{array}{l} (1) | \vec{a} | \geq 0 \\ (2) | r \vec{a} | = | r | \cdot | \vec{a} | \\ (3) | \vec{a} + \vec{b} | \leq | \vec{a} | + | \vec{b} | \end{array}$

Der Betrag eines Vektors $\vec{a}$ kann auch rein vektoriell ohne expliziten Rückgriff auf die Koordinaten der Endpunkte eines ihn repräsentierenden Pfeils berechnet werden. Wird der Vektor $\vec{a}$ als Ortsvektor bezüglich des Koordinatenursprungs O dargestellt, so ist mit
$\vec{a} = \vec{O A} = (\begin{matrix} a_{x} \\ a_{y} \end{matrix}) b z w . \vec{a} = \vec{O A} = (\begin{matrix} a_{x} \\ a_{y} \\ a_{z} \end{matrix})$
eine gerichtete Strecke gegeben, deren Länge gleich dem Betrag von $\vec{a}$ ist.

Betrag eines Ortsvektors

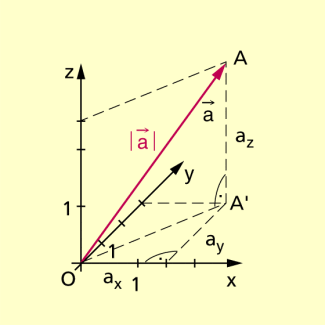
Durch Anwenden des Satzes des PYTHAGORAS im ebenen Fall und zweimaliges Anwenden dieses Satzes im räumlichen Fall erhält man für den Betrag des Vektors $\vec{a}$ :
$\begin{matrix} | \vec{a} | = \sqrt{a_{x}^{2} + a_{y}^{2}} b z w . \\ | \vec{a} | = \sqrt{a_{x}^{2} + a_{y}^{2} + a_{z}^{2}} \end{matrix}$

Soll der Betrag eines Vektors berechnet werden, der durch einen Pfeil $\vec{P_{1} P_{2}}$ repräsentiert wird, so bestimmt man analog den Betrag des Vektors ${\vec{p}}_{2} - {\vec{p}}_{1}$

Berechnung des Betrags eines durch Ortsvektoren gegebenen Vektors

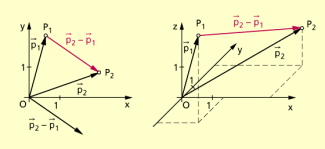
Mit
${\vec{p}}_{2} - {\vec{p}}_{1} = (\begin{matrix} x_{2} - x_{1} \\ y_{2} - y_{1} \end{matrix}) b z w . {\vec{p}}_{2} - {\vec{p}}_{1} = (\begin{matrix} x_{2} - x_{1} \\ \begin{matrix} y_{2} - y_{1} \\ z_{2} - z_{1} \end{matrix} \end{matrix})$
ergibt sich:
$\begin{array}{l} | {\vec{p}}_{2} - {\vec{p}}_{1} | = \sqrt{{(x_{2} - x_{1})}^{2} + {(y_{2} - y_{1})}^{2}} b z w . \\ | {\vec{p}}_{2} - {\vec{p}}_{1} | = \sqrt{{(x_{2} - x_{1})}^{2} + {(y_{2} - y_{1})}^{2} + {(z_{2} - z_{1})}^{2}} \end{array}$

$| {\vec{p}}_{2} - {\vec{p}}_{1} |$ gibt dabei zugleich die Länge der Strecke $\bar{P_{1} P_{2}}$ an.

Beispiel 2: Es ist der Betrag des Vektors $\vec{a}$ zu bestimmen, der durch den Pfeil mit den Endpunkten
${\vec{p}}_{1} = (\begin{matrix} - 2 \\ - 1 \\ - 4 \end{matrix}) u n d p_{2} = (\begin{matrix} 2 \\ 5 \\ 7 \end{matrix})$
repräsentiert wird.

Nach obiger Formel gilt:
$\begin{array}{l} | \vec{a} | = | {\vec{p}}_{2} - {\vec{p}}_{1} | \\ = \sqrt{{(2 - (- 2))}^{2} + {(5 - (- 1))}^{2} + {(7 - (- 4))}^{2}} = \sqrt{173} \end{array}$

Stand: 2010
Dieser Text befindet sich in redaktioneller Bearbeitung.

Mathe Note verbessern?

Kostenlos bei Duden Learnattack registrieren und ALLES 48 Stunden testen.

Kein Vertrag. Keine Kosten.

40.000 Lern-Inhalte in Mathe, Deutsch und 7 weiteren Fächern
Hausaufgabenhilfe per WhatsApp
Original Klassenarbeiten mit Lösungen
Deine eigene Lern-Statistik
Kostenfreie Basismitgliedschaft

Mathe kostenlos lernen

Verwandte Artikel

Betrag eines Vektors

Rechtliches

Einloggen