Die gaußsche Glockenkurve

Im Verlauf des 18. Jahrhunderts wurde insbesondere durch die enorme Verbesserung der Messinstrumente vor allem bei Astronomen, Physikern und Geodäten das Bewusstsein geschärft, dass Messfehler wohl grundsätzlich nicht vermeidbar sind. Zugleich wuchs damit aber auch das Bedürfnis nach einer quantitativen Bestimmung von Messfehlern, insbesondere in der Form einer Messfehlerverteilung.

GAUSS stellte sich dieser aus der Praxis kommenden Herausforderung, wobei er ein allgemeineres Fehlerkonzept zugrunde legte als das des Messfehlers. Dies begründete die Ausstrahlungskraft seiner dazu verfassten wissenschaftlichen Arbeiten. Zugleich beeindruckte nachfolgende Mathematikergenerationen wohl auch die Art und Weise seiner Problemlösung. Unter der Annahme einiger intuitiv einsichtiger mathematischer Einschränkungen über die gesuchte Fehlerverteilung leitete er durch ein streng mathematisch-analytisches Vorgehen die Normalverteilung als Fehlerverteilung her.

Die Rechnungen führten GAUSS zu einem Typ von Glockenkurven, die Gleichungen der folgenden Gestalt genügen:
$g\left(x\right)=\chi \cdot e^{-k{x}^2}(mit\chi ,k\in {ℝ}^{+})$

Die Funktionen dieser Glockenkurven, die bei x = 0 einen Maximumpunkt haben und dazu zwei symmetrisch gelegene Wendepunkte besitzen, sind im Allgemeinen noch keine Wahrscheinlichkeitsdichten, da sie nicht auf 1 normiert sind. Erforderlich ist also eine entsprechende Parameterbestimmung.

Der Einfachheit wegen kann man fordern, dass die Wendestellen bei x = –1 und x = 1 liegen sollen. Damit lässt sich k bestimmen. Es ist:
$\begin{array}{l}g\text{'}\left(x\right)=-2k\chi x{e}^{-k{x}^2}\\ g\text{'}\text{'}\left(x\right)=\left(4k^2\chi x^2-2k\chi \right)e^{-k{x}^2}\end{array}$

Aus der Forderung $g\text{'}\text{'}\left(-1\right)=g\text{'}\text{'}\left(1\right)=2k\chi \left(2k-1\right)e^{-k}=0$ folgt dann $k=\frac{1}{2}$.

Nun lässt sich $\chi$ aus der für Wahrscheinlichkeitsdichten notwendigerweise geltenden Bedingung
${\displaystyle \underset{-\infty }{\overset{\infty }{\int }}\chi \cdot e^{-\frac{1}{2}{x}^2}dx}=1$
berechnen.

Unter Verwendung von
${\displaystyle \underset{-\infty }{\overset{\infty }{\int }}{e}^{-\frac{1}{2}{x}^2}dx}=\sqrt{2\pi }$
ergibt sich $\chi =\frac{1}{\sqrt{2\pi }}$.

Wir definieren nun wie folgt:

• Der Graph der durch $\varphi \left(x\right)=\frac{1}{\sqrt{2\pi }}{e}^{-\frac{1}{2}{x}^2}$ für alle $x\in ℝ$ definierten Dichtefunktion $\varphi$ heißt gaußsche Glockenkurve.

Die Dichtefunktion hat folgende Eigenschaften:

1. $\varphi$ ist eine gerade Funktion, d.h., für alle $x\in ℝ$ gilt:
   $\varphi \left(x\right)=\varphi \left(-x\right)$
2. $\varphi$ ist stetig und beliebig oft differenzierbar mit $D_{\varphi }=ℝ$ und $W_{\varphi }={ℝ}^{+}$.
3. Der Graph von $\varphi$ hat genau einen Maximumpunkt:
   $H\left(0;\frac{1}{\sqrt{2\pi }}\right)=H\left(0;\approx \mathrm{0,4}\right)$
4. Der Graph von $\varphi$ hat die Wendepunkte $W_{1;2}\left(\pm 1;\frac{1}{\sqrt{2\pi e}}\right)=W_{1;2}\left(\pm 1;\approx \mathrm{0,24}\right)$.
5. Die x-Achse ist Asymptote des Graphen von $\varphi$, d.h., es gilt:
   $\underset{x\to \pm \infty }{\lim }\varphi \left(x\right)=0$
6. Für $x<0$ ist $\varphi$ streng monoton wachsend, für $x>0$ streng monoton fallend.

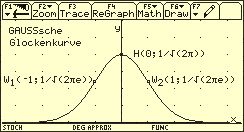
Es gibt auch andere Glockenkurven, z.B. den Graphen von g mit $g\left(x\right)=\frac{1}{\pi \left(1+x^2\right)}$.

Obwohl deren Graph kaum von der gaußschen Glockenkurve abzuweichen scheint, besitzt eine Zufallsgröße X mit der Dichtefunktion g eine unendliche Streuung.

Sollte es notwendig sein, den Graphen der gaußschen Glockenkurve zu zeichnen, ohne dass weitere Hilfsmittel zur Verfügung stehen, dann können die folgenden leicht zu merkenden Überschlagswerte hilfreich sein: