Differenzen- und Differenzialgleichungen

Die Gleichung $a_{i+1}=q\cdot a_i$ bzw. die umgestellte Form $a_{i+1}-a_i=(q-1)a_i$ ist eine einfache Differenzengleichung: Sie beschreibt die Änderung des Wertes der Folgenglieder in Abhängigkeit vom Index i und von anderen Folgengliedern. Eine Lösung dieser Gleichung ist die Folge $(a_i)mit{a}_i=s{q}_i,$ was man durch Einsetzen in die Differenzengleichung überprüfen kann.

Auch für Differenzialgleichungen kann man anhand bekannter Inhalte leicht ein Beispiel finden. So gilt für die Ableitung der Funktion $y=f(x)=e^{x}mitx\in ℝ$ die Beziehung $y^{\prime }=f^{\prime }(x)=e^x.$Daraus folgt $f(x)=e^x=f^{\prime }(x)oderkürzer{f}^{\prime }(x)=f(x).$

Dies ist eine Differenzialgleichung, sie beschreibt die Funktion $y=f(x)$ durch die markante Eigenschaft, dass Funktionswert und Ableitungswert stets gleich sind. Eine Lösung der angegebenen Differenzialgleichung ist natürlich die Funktion $y=e^x$, was wiederum durch Einsetzen überprüft werden kann.

Differenzen- und Differenzialgleichungen stehen in einem engen Zusammenhang.

Wird in der Differenzialgleichung
$f^{\prime }(x)=f(x)$
der Differenzialquotient
$f^{\prime }(x)=\underset{h\to 0}{\lim }\frac{f(x+h)-f(x)}{h}$
näherungsweise durch den Differenzenquotienten
$\frac{f(x+h)-f(x)}{h}$
mit sehr kleinem h ersetzt, so erhält man die Gleichung
$\frac{f(x+h)-f(x)}{h}=f(x)oderf(x+h)=f(x)+hf(x)=(1+h)f(x)$.

Die Gleichung $f(x+h)=(1+h)f(x)$ besagt, dass sich der Funktionswert $f(x+h)$ an der Stelle $x+h$ als Produkt von $f(x)und(1+h)$ ergibt. Multipliziert man den Wert $f(x+h)$ wiederum mit $(1+h),$ so erhält man $f(x+2h).$ Auf diesem Weg kann ausgehend von einem bekannten Funktionswert eine Näherungslösung der Differenzialgleichung schrittweise aufgebaut werden.

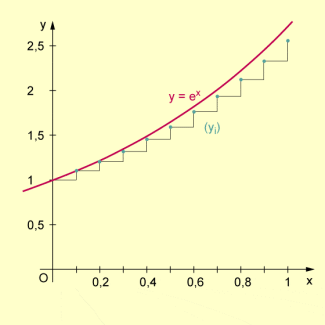
Dabei entsteht die Folge $(y_i)$ von Funktionswerten, die durch die rekursive Bildungsvorschrift $y_{i+1}=(1+h)y_i$, also durch eine Differenzengleichung, beschrieben wird. In der Abbildung ist $f(x)=e^x$ als Lösung der Differenzialgleichung $f^{\prime }(x)=f(x)$ und die Folge $(y_i)$ als Lösung der Differenzengleichung $y_{i+1}=(1+h)y_{i}fürh=\mathrm{0,1}und{y}_0=f(0)=1$ dargestellt.

Generell gilt, dass der Zusammenhang zwischen Differenzen- und Differzialgleichungen durch die Unterschiede, Ähnlichkeiten und Gemeinsamkeiten zwischen Differenzen- und Differenzialquotienten geprägt ist.

Differenzengleichungen bieten einen elementaren mathematischen Zugang zu anspruchsvollen praktischen Fragestellungen, z.B. aus der Populationsdynamik, der Finanzmathematik und der Technik. Sogar komplexe dynamische Systeme werden heute unter Zuhilfenahme von Differenzengleichungssytemen simuliert und untersucht.
(Dynamische Systeme sind Systeme, deren Elemente sich ständig ändern, wobei die Struktur des Systems jedoch erhalten bleibt. Die meisten der Systeme, in die der Mensch einbezogen ist, wie Sozialsysteme, Wirtschaftssysteme, Ökosysteme, technische Systeme, besitzen diese Eigenschaft.) Dabei setzt das Bearbeiten von Differenzengleichungen lediglich eine gewisse Gewandtheit in der Buchstabenrechnung voraus. Es umfasst im Wesentlichen das Abarbeiten von iterativen Berechnungsverfahren und rekursiven Bildungsvorschriften, das Finden expliziter Bildungsvorschriften für Folgen, das Lösen von Gleichungssystemen und ähnlich elementare Anforderungen.

In der Geschichte der Mathematik tauchen Differenzengleichungen ab dem 12./13. Jahrhundert auf. Mit der erfolgreichen Entwicklung der Algebra und Arithmetik (Einführung komplexer Zahlen, Lösen von Gleichungen auch höheren Grades, Verbesserung des Gleichungskalküls, Gleichungssysteme) wuchsen in der Folgezeit auch die Möglichkeiten zur Bearbeitung anspruchsvollerer Differenzengleichungen.
Beginnend in der Mathematik der Renaissance, vor allem aber im 17. Jahrhundert entfalteten sich angeregt durch breites, oft praktisch begründetes Interesse an der Mechanik Vorüberlegungen zur Differenzial- und Integralrechnung. Diese Entwicklung gipfelte in der Schaffung des Kalküls der Infinitesimalrechnung durch GOTTFRIED WILHELM LEIBNIZ (1646 bis 1727) in den Jahren 1673 bis 1676.

Die Beschäftigung mit Differenzialgleichungen war Bestandteil der Entstehung der Infinitesimalrechnung. Die Mathematiker spürten, dass der neue Kalkül hervorragend auf Fragen anwendbar war, die man bisher mit Differenzengleichungen bearbeitete. In der Folgezeit wurden eine Reihe von Differenzialgleichungstypen durch geschickten Einsatz des Kalküls der Differenzialrechnung gelöst und auf physikalische und technische Probleme angewandt, wobei man Differenzengleichungen als numerische Lösungsverfahren für Differenzialgleichungen verwendete und weiterentwickelte.

In den letzten Jahrzehnten hat die Anwendung von Differenzial- und in deren Gefolge vor allem von Differenzengleichungen deutlich zugenommen. Zwei Gründe lassen sich dafür finden:

1. Zum einen standen immer leistungsfähigere Rechner zur Verfügung, die die numerische Behandlung von Differenzengleichungssystemen zunehmend besser bewältigten. Durch deren Einsatz konnten immer komplexere, auch nichtlineare Differenzengleichungssysteme bearbeitet werden.
2. Zum anderen wandte die Wissenschaft bei der Untersuchung unserer Umwelt zunehmend komplexere Betrachtungsweisen an. Dynamische Systeme fanden mehr und mehr Interesse wie Aufmerksamkeit der Wissenschaftler, wobei Differenzial- und Differenzengleichungssysteme sich als entscheidende mathematische Instrumente zur Bewältigung damit verbundener Probleme erwiesen. Das wohl bekannteste Ergebnis derartiger Untersuchungen ist der „Bericht des Club of Rome zur Lage der Menschheit“, bekannt vor allem als Buchtitel „Grenzen des Wachstums“ (1972). Die Grundlagen für den Bericht legte Professor DENNIS MEADOWS mit einer Gruppe internationaler Wissenschaftler am MIT („Massachusetts Institute of Technologie“) mittels Simulation dynamischer Systeme.