Direkt zum Inhalt

Differenzialgleichungen zur Beschreibung des elektromagnetischen Schwingkreises

Ein elektromagnetischer Schwingkreis ist ein geschlossener Stromkreis, in dem ein Kondensator und eine Spule (mit induktivem und ohmschem Widerstand - in der folgenden Abbildung der Übersichtlichkeit halber getrennt gezeichnet) in Reihe geschaltet sind.

Schule wird easy mit KI-Tutor Kim und Duden Learnattack

  • Kim hat in Deutsch, Mathe, Englisch und 6 weiteren Schulfächern immer eine von Lehrkräften geprüfte Erklärung, Video oder Übung parat.
  • 24/7 auf Learnattack.de und WhatsApp mit Bildupload und Sprachnachrichten verfügbar. Ideal, um bei den Hausaufgaben und beim Lernen von Fremdsprachen zu unterstützen.
  • Viel günstiger als andere Nachhilfe und schützt deine Daten.
Jetzt 30 Tage risikofrei testen

Bild

Da es sich um einen geschlossenen Stromkreis ohne Spannungsquelle handelt, gilt:
U I N + U R + U C = 0   b z w .   L ⋅ l ′ ( t ) + R ⋅ I ( t ) + Q ( t ) C = 0 (1)

Da Q ′ ( t ) = I ( t ) gilt, erhält man durch Differenzieren der Gleichung (1) folgende Differenzialgleichung:
L ⋅ l ″ ( t ) + R ⋅ I ′ ( t ) + I ( t ) C = 0 bzw. l ″ ( t ) + R L l ′ ( t ) + 1 L C l ( t ) = 0 (2)

Hierbei handelt es sich um eine lineare homogene Differenzialgleichung 2. Ordnung mit konstanten Koeffizienten der Form
f ″ ( x ) + q f ′ ( x ) + r   f ( x ) = 0   m i t   q = R L   u n d   r = 1 L C .

Als Lösungsansatz verwendet man die Exponentialfunktion f ( x ) = e k x , für die k zu bestimmen ist. Die Gleichung zur Bestimmung von k heißt die charakteristische Gleichung der Differenzialgleichung.

Die zur Differenzialgleichung (2) gehörende charakteristische Gleichung lautet k 2 + R L k + 1 L C = 0 mit der Lösung k 1 / 2 = − R 2 L ± R 2 4 L 2 − 1 L C . (3)

Mit den Lösungen k 1   u n d   k 2 erhält man als allgemeine Lösung der Differenzialgleichung f ″ ( x ) + q f ′ ( x ) + r   f ( x ) = 0   m i t   q = R L   u n d   r = 1 L C :

f ( x ) = { c 1 ⋅ e k 1 x + c 2 ⋅ e k 2 x f ü r   r < q 2 4 c 1 ⋅ e k x + c 2 ⋅ x ⋅ e k x c 1 ⋅ e − q 2 ⋅ x cos ω x + c 2 ⋅ e − q 2 ⋅ x sin ω x f ü r   r = q 2 4 ,   k 1 = k 2 = k f ü r   r > q 2 4 ,   ω = r − q 2 4 }       m i t   c 1 ,   c 2   k o n s tan t

Demnach hängt das Lösungsverhalten vom Größenvergleich zwischen r = 1 L C   u n d   q 2 4 = R 2 4 L 2 ab.

Beispiel

Es wird ein Schwingkreis betrachtet mit L = 0,1   H = 0,1 V s A   u n d   C = 10   μ F = 10 − 5 F = 10 − 5 A s V .

Für den Fall reeller Doppellösungen in Gleichung (3) erhält man R 2 4 L 2 = 1 L C und daraus R = 200 Ω .

Im Weiteren werden vier Fälle betrachtet:

  R 1 = 800 Ω R 2 = 200 Ω
Lösungen der char. Gleichungzwei reelle Lösungen k 1 = − 127,02 s − 1 k 2 = − 7872,98 s − 1 eine reelle Doppellösung k = − 1000 s − 1
Kreisfrequenzkeine Schwingungkeine
Schwingung
allg. Lösung der
Differenzialgl.		 l 1 ( t ) = c 1 e − 127,02 s − 1 ⋅ t + c 2 e − 7872,98 s − 1 ⋅ t l 2 ( t ) = ( c 1 + c 2 t ) ⋅ e − 1000 s − 1 ⋅ t

 

  R 3 = 50 Ω R 4 = 0 Ω
Lösungen der char. Gleichungzwei komplexe Lösungenzwei komplexe
Lösungen
Kreisfrequenz ω = 968,25 s − 1 ω = 1000 s − 1
allg. Lösung der
Differenzialgl.		 l 3 ( t ) = e − 250 s − 1 ⋅ t ( c 1 cos 968,25 s − 1 t     + c 2 sin 968,25 s − 1 t ) l 4 ( t ) = c 1 cos 1000 s − 1 t + c 2 sin 1000 s − 1 t

Als partikuläre Lösung für U C ( 0 ) = 10 V ,   l ( 0 ) = 0 ergeben sich dann:

K r i e c h f a l l : l 1 ( t ) = − 0,0129 A ⋅ e − 127,02 s − 1 ⋅ t + 0,0129 A ⋅ e − 7872,98 s − 1 ⋅ t   a p e r i o d i s c h e r   G r e n z f a l l : l 2 ( t ) = − 100 A s − 1 t ⋅ e − 1000 s − 1 ⋅ t   g e d ä m p f t e   S c h w i n g u n g e n : I 3 ( t ) = e − 250 s − 1 ⋅ t ⋅ 0,1033 A   sin 968,25 s − 1 t   u n g e d ä m p f t e   S c h w i n g u n g e n : l 4 ( t ) = − 0,1 A   sin 1000 s − 1 t  

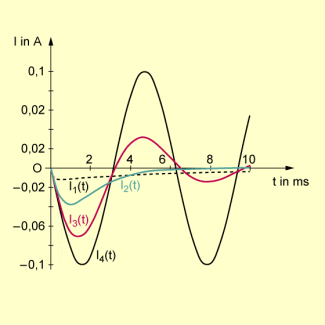
Hinweis: Wenn l = 0,   d a n n   i s t   U R = 0,   a l s o   U I N = − U C = − 10 V und damit l ′ ( 0 ) = − 10 V 0,1 H = − 100 A s − 1 .

Die Stromstärkeverläufe für die vier verschiedenen Widerstände sind in der folgenden Abbildung grafisch dargestellt. Man erkennt, wie sich die wachsenden Widerstandsgrößen auf die Kurven für die zugehörigen Stromstärken auswirken.

  • Lösungen der linearen Differenzialgleichung
Lernhelfer (Duden Learnattack GmbH): "Differenzialgleichungen zur Beschreibung des elektromagnetischen Schwingkreises." In: Lernhelfer (Duden Learnattack GmbH). URL: http://www.lernhelfer.de/schuelerlexikon/mathematik-abitur/artikel/differenzialgleichungen-zur-beschreibung-des (Abgerufen: 29. June 2025, 17:17 UTC)

Suche nach passenden Schlagwörtern