Geometrische Wahrscheinlichkeit

Gutta cavat lapidem – Steter Tropfen höhlt den Stein.

Beispiel: Mit Freude und Stolz zieht Familie Tüchtig in ihr neues Einfamilienhaus ein. Als es regnet, wird ihre Stimmung etwas getrübt, denn die Dachrinne ist an einer Stelle nicht dicht. Nur Jonas beobachtet mit Interesse, wie die aus sieben Meter Höhe herabfallenden Wassertropfen immer an einer anderen Stelle aufschlagen. Aber der dort liegende kleine Stein wird nicht getroffen. Rings um ihn fallen die Tropfen zur Erde. Dann erwischt es ihn aber doch. Wie könnte man die Trefferwahrscheinlichkeit berechnen, fragt sich Jonas.

Ihm fällt dazu der folgende Formelansatz aus dem Stochastikunterricht ein:
$\frac{\text{günstige}\text{Fälle}}{\text{mögliche}\text{Fälle}}$

Vielleicht sollte man, so denkt Jonas, für die Trefferwahrscheinlichkeit deshalb das nachstehende Verhältnis bestimmen:
$\frac{\text{günstige}Trefferfläche}{\text{mögliche}Trefferfläche}$

Dies führt zum Begriff der geometrischen Wahrscheinlichkeit:

• Definition: Ist die Ergebnismenge $\Omega$ ein endliches Flächenstück mit dem Inhalt $A_{\Omega }$ und ist E eine Teilfläche von $\Omega$ mit dem Inhalt $A_E$, so heißt das Verhältnis $P\left(E\right)=\frac{A_E}{A_{\Omega }}$ geometrische Wahrscheinlichkeit des Ereignisses E.

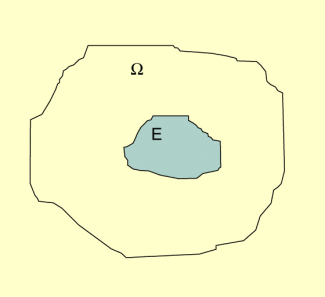
Die geometrische Wahrscheinlichkeit $P\left(E\right)$ ist unabhängig von der konkreten Form und Lage der Teilfläche E. Sie ist das Verhältnis des Flächeninhalts der für das Ereignis günstigen Teilfläche zum Flächeninhalt der möglichen Grundfläche. In dieser Formulierung wird die Verwandtschaft zur LAPLACE-Regel deutlich:

• Das der LAPLACE-Regel zugrunde liegende Prinzip der Gleichwahrscheinlichkeit kommt bei der geometrischen Wahrscheinlichkeitsverteilung darin zum Ausdruck, dass Ereignissen, denen Flächenstücke mit gleichem Flächeninhalt entsprechen, die gleiche Wahrscheinlichkeit zukommt.

Anmerkung: Es ist zu beachten, dass die Bezeichnungen „geometrische Wahrscheinlichkeit“ und „geometrische Verteilung“ zwar ähnlich klingen, aber für verschiedene Zufallsexperimente verwendet werden.

Die oben angeführte Nähe zum sogenannten klassischen Zugang zur Wahrscheinlichkeit (LAPLACE-Wahrscheinlichkeit) darf die Sonderstellung der geometrischen Wahrscheinlichkeit nicht überdecken, was an den folgenden Beispielen demonstriert werden soll.

Beispiel 1: Ein zufällig herabfallender Wassertropfen habe als mögliche Trefferfläche $\Omega$ einen Kreis mit dem Radius r.
Mit welcher Wahrscheinlichkeit trifft der Wassertropfen auf einen Kreissektor E mit einem Öffnungswinkel von 120°?

Lösung:
$P\left(E\right)=\frac{A_E}{A_{\Omega }}=\frac{\frac{120}{360}\cdot \pi r^2}{\pi r^2}=\frac{1}{3}$

Interessant ist die Ergebnismenge dieses Zufallsexperiments. Jedes mögliche Ergebnis werde durch einen Punkt $\left(\alpha ;a\right)$ mit $0^{\circ }\le \alpha <{360}^{\circ }$ und $0\le a\le r$ (als mathematisches Modell eines Regentropfens) der Kreisfläche beschrieben, d.h. es sind überabzählbar unendlich viele Ergebnisse möglich. Bei der LAPLACE-Wahrscheinlichkeit dagegen besteht die Ergebnismenge nur aus endlich vielen Elementen.

Beispiel 2: Die mögliche Trefferfläche eines zufällig herabfallenden Wassertropfens sei ein Quadrat mit der Seitenlänge a.
Gesucht ist die Wahrscheinlichkeit p, dass der Wassertropfen auf den eingeschrieben Kreis fällt.

Lösung:
$p=\frac{\pi {\left(\frac{a}{2}\right)}^2}{a^2}=\frac{\pi }{4}$

Das Ergebnis ist keine rationale Zahl. Während beim klassischen Zugang (zur Wahrscheinlichkeitsrechnung) Wahrscheinlichkeiten stets rationale Zahlen sind, können geometrische Wahrscheinlichkeiten auch irrationale Zahlen sein.

Beispiel 3: Für einen „auf gut Glück“ herabfallenden Wassertropfen gilt nebenstehendes Treffergebiet.
Wie groß ist die Wahrscheinlichkeit p für einen Treffer?

Lösung(en):
$\begin{array}{l}p=\frac{\pi {\left(\frac{r}{2}\right)}^2}{\pi r^2}=\frac{1}{4}(Variante1)\\ p=\frac{r}{2r}=\frac{1}{2}(Variante2)\end{array}$

Die Ursache für die unterschiedlichen Ergebnisse liegt in der ungenauen Beschreibung des Zufallsexperiments.

Bei der Variante 1 ist die mögliche Trefferfläche der Kreis mit dem Durchmesser 2r und gesucht ist die Wahrscheinlichkeit, dass der Wassertropfen auf die Kreisfläche mit dem Durchmesser r fällt.

Bei der Variante 2 ist die mögliche Trefferfläche die Strecke mit der Länge 2r und gesucht ist die Wahrscheinlichkeit, dass der Wassertropfen auf die Strecke mit der Länge r fällt.

Das Beispiel zeigt, dass geometrische Wahrscheinlichkeiten auch im ${ℝ}^1$ (und analog im ${ℝ}^3$) betrachtet werden können. Dabei handelt es sich aber jeweils um verschiedene Zufallsexperimente, deren Vermengung zu Fehldeutungen führen kann.

Im Zusammenhang mit der geometrischen Wahrscheinlichkeit ist es in der Geschichte der Wahrscheinlichkeitstheorie noch zu anderen Fehlschlüssen gekommen. Das wohl bekannteste Beispiel dafür ist das bertrandsche Paradoxon.

Durch Simulation des zufälligen Auftretens eines Punktes auf eine Fläche kann die geometrische Wahrscheinlichkeit zum näherungsweisen Berechnen auch komplizierterer Flächeninhalte genutzt werden. Aus der Geschichte der Wahrscheinlichkeitstheorie ist hierzu vor allem die als buffonsches Nadelexperiment bezeichnete bekannt. Diese ermöglicht auch eine experimentelle Bestimmung der Zahl $\pi$.