Indirekter Beweis

Beim indirekten Beweis eines Satzes der Form $A\Rightarrow B$ geht man von der Annahme aus, dass die Behauptung B falsch sei und deren Negation $\neg B$ also wahr ist. Aus dieser Annahme versucht man, einen Widerspruch herzuleiten. Wenn das gelingt, dann wäre $\neg B$ falsch und somit B wahr.

Das Erzeugen des Widerspruchs kann in unterschiedlicher Weise geschehen.
Im Allgemeinen unterscheidet man folgende Fälle:
(1) Es ergibt sich $\neg A$, d.h. ein Widerspruch zur gültigen Voraussetzung A. Das ist in zweierlei Weise möglich:

1. Aus dem Gegenteil der Behauptung folgt unmittelbar das Gegenteil der Voraussetzung, d.h.:
   $A\Rightarrow B\iff \neg B\Rightarrow \neg A$
   (die sogenannte Kontraposition eines Satzes)
2. Aus der Voraussetzung und dem Gegenteil der Behauptung ergibt sich das Gegenteil der Voraussetzung, d.h.
   $A\Rightarrow B\iff \left[A\wedge \neg B\right]\Rightarrow \neg A$

(2) Aus der Voraussetzung und dem Gegenteil der Behauptung ergibt sich die Behauptung, d.h. ein Widerspruch zur negierten Behauptung:
$A\Rightarrow B\iff \left[A\wedge \neg B\right]\Rightarrow B$

$$(3) Aus der Voraussetzung und dem Gegenteil der Behauptung ergibt sich eine neue Aussage der Form $C\wedge \neg C$, wobei C eine bereits als wahr erkannte Aussage darstellt. Man spricht in diesem Fall von einer reductio ad absurdum, es handelt sich um einen Widerspruch zu einem bereits bewiesenen Satz:
$A\Rightarrow B\iff \left[A\wedge \neg B\right]\Rightarrow \left[C\wedge \neg C\right]$

In jedem dieser drei (bzw. besser vier) Fälle ergibt sich eine Implikation, die zu $A\Rightarrow B$ äquivalent ist (durch Aufstellen der Wahrheitswertetabellen überzeugt man sich sehr schnell von der Gültigkeit der Äquivalenzen).

Damit ergibt sich folgende Struktur für den indirekten Beweis:
Aus der Voraussetzung, bereits bekannten Tatsachen (Definitionen und Lehrsätze) und dem Gegenteil der Behauptung wird mithilfe einer endlichen Anzahl gültiger Schlussregeln ein Widerspruch zur Voraussetzung zu bereits bekannten Tatsachen oder zum Gegenteil der Behauptung erzeugt.
Gelingt die Widerspruchserzeugung, dann ist das Gegenteil der Behauptung falsch und somit nach dem Satz vom ausgeschlossenen Widerspruch sowie dem Satz vom ausgeschlossenen Dritten die Behauptung wahr.
Die beiden genannten Schlussregeln bilden also gewissermaßen das Fundament für den indirekten Beweis.

Im Folgenden betrachten wir zwei Beispiele.

Beispiel 1

• Wenn das Quadrat einer natürlichen Zahl gerade ist, so ist auch die Zahl selbst gerade.

1. Voraussetzung:
   $2|x^2;x\in \mathbb{N}$
2. Behauptung:
   $2|x$
3. Beweis (indirekt):
   Das Gegenteil der Behauptung ist $2\cancel{I}x$ (2 teilt nicht x).

Damit ist ein Widerspruch zur Voraussetzung erzeugt, d.h., das Gegenteil der Behauptung ist falsch, und somit ist die Behauptung bzw. der Satz wahr.

Beispiel 2

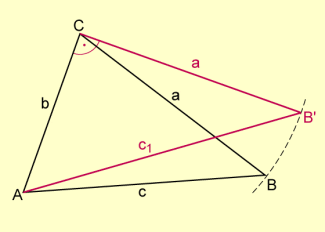
• Gilt für die Maßzahlen der Seiten eines Dreiecks ABC die Beziehung $a^2+b^2=c^2$, dann ist das Dreieck rechtwinklig (Umkehrung des Satzes von PYTHAGORAS).

1. Voraussetzung:
   beliebiges Dreieck ABC mit $a^2+b^2=c^2$
2. Behauptung:
   $\sphericalangle BCA=90°$
3. Beweis (indirekt):
   Annahme: $\gamma \ne 90°$

Feststellung	Begründung
$△AB\text{'}C$ ist rechtwinklig.	Senkrechte zu AC in C und von C aus a abtragen
$a^2+b^2=c_1{}^2(1)$	Satz des PYTHAGORAS für rechtwinkliges Dreieck AB'C
$a^2+b^2=c^2(2)$	nach Voraussetzung
Wegen $c\ne c_1$ können (1) und (2) nicht gleichzeitig gelten.

Damit ergibt sich ein Widerspruch zur Voraussetzung, die Annahme ist also falsch und somit die Behauptung war, d.h., es ist $\gamma =90°$.

Das letzte Beispiel macht zweierlei deutlich: Erstens der indirekte Beweis wird vorwiegend beim Beweis der Umkehrung von Sätzen angewendet. Zweitens wird dabei der ursprüngliche Beweis häufig als Beweismittel verwendet.

Weitere Anwendungsbereiche des indirekten Beweises sind die folgenden:

• Nachweis von Eindeutigkeitsaussagen, etwa
  Es gibt höchstens ein x mit der Eigenschaft $H\left(x\right)$.
  (Die Annahme der Existenz eines zweiten Elements wird ad absurdum geführt.)
• Nachweis von negierten Existentialaussagen, etwa
  Es gibt kein x mit der Eigenschaft $H\left(x\right)$.
  (Man weist nach, dass doch ein Element existiert, indem man eines konstruiert.)