Intervallschachtelungen

Unter einem abgeschlossenen Intervall $\left[a;b\right]$ versteht man bekanntlich eine Teilmenge einer Zahlenmenge M, die aus allen Zahlen x besteht, die folgende Bedingungen erfüllen:
$x,a,b\in Munda\le x\le b$
(Damit gehören beide Randpunkte a und b zum Intervall. Ist dies nicht der Fall, spricht man von einem offenen bzw. halboffenen Intervall.)

Den Begriff der Intervallschachtelung definieren wir nun folgendermaßen:

• Eine Folge von abgeschlossenen Intervallen $\left[a_1;b_1\right],\left[a_2;b_2\right],\left[a_3;b_3\right],\mathrm{...}$ mit $\left[a_{n+1};b_{n+1}\right]\subseteq \left[a_n;b_n\right]$ für alle $n\in \mathbb{N}$ heißt Intervallschachtelung, wenn die Intervalllängen $b_n-a_n$ mit wachsendem n immer kleiner werden und unter jede noch so kleine Schranke sinken.

Es gilt dann $a_1\le a_2\le \mathrm{...}\le a_n\le b_n\le \mathrm{...}\le b_2\le b_1$ für alle n und die Folge $\left(b_n-a_n\right)$ ist eine Nullfolge.

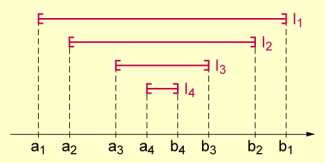
In der Menge $\mathbb{N}$ der natürlichen Zahlen und in der Menge $\mathbb{Z}$ der ganzen Zahlen lassen sich solche Intervallschachtelungen, bei denen das folgende Intervall immer eine Teilmenge des vorhergehenden ist und bei denen die Intervalllängen immer kleiner werden, nicht bilden, da die Intervalllänge 1 nicht unterschritten werden kann.

In der Menge $\mathbb{Q}$ der rationalen Zahlen dagegen lassen sich solche Intervallschachtelungen bilden, da die rationalen Zahlen überall dicht liegen. Damit ist die Bedingung, dass die Folge $\left(b_n-a_n\right)$ eine Nullfolge ist, erfüllbar.

Jede Intervallschachtelung in $\mathbb{Q}$ besitzt nun einen Kern c mit $a_n\le c\le b_n$ für alle $n\in \mathbb{N}$. Dieser Kern ist eine reelle Zahl.
Wir betrachten dazu zwei Beispiele:

Wie Beispiel 2 zeigt, muss der Kern einer Intervallschachtelung in der Menge $\mathbb{Q}$ der rationalen Zahlen nicht immer selbst eine rationale Zahl sein.

Durch eine Intervallschachtelung wird aber genau eine reelle Zahl (als Kern) definiert. Die Existenz eines Kernes ist gesichert, weil $a_n=c=b_n$ möglich ist. Die Eindeutigkeit ergibt sich daraus, dass die Annahme zweier verschiedener Kerne $c_{1}und{c}_2$ im Widerspruch zu der Bedingung steht, dass $\left(b_n-a_n\right)$ eine Nullfolge ist.

In der Menge $ℝ$ der reellen Zahlen besitzt jede Intervallschachtelung als Kern eine reelle Zahl. Damit ist die Menge der reellen Zahlen abgeschlossen, d.h. eine Erweiterung ohne Verzicht auf wesentliche Eigenschaften ist nicht mehr möglich.

Die Verknüpfung reeller Zahlen (das Rechnen mit ihnen) kann man nun mithilfe der sie definierenden Intervallschachtelungen erklären. Dabei zeigt sich, dass man mit reellen Zahlen wie mit rationalen Zahlen rechnen kann. Insbesondere gelten solche Gesetzmäßigkeiten wie die Kommutativ- und Assoziativgesetze der Addition und Multiplikation sowie das Distributivgesetz.