Periodizität von Funktionen

In Natur und Technik treten periodische Vorgänge auf. Zu ihrer Beschreibung sind die trigonometrischen Funktionen von besonderer Bedeutung. Diese Klasse von Funktionen wird durch eine weitere Eigenschaft charakterisiert, die Periodizität.

Die Graphen periodischer Funktionen sind verschiebungssymmetrisch, sie gehen durch Verschiebung längs der x-Achse mit einer Verschiebungsweite p oder $k \cdot p$ in sich über.

Die bekanntesten periodischen Funktionen sind die trigonometrischen Funktionen. Die Sinusfunktion und die Kosinusfunktion sind periodisch mit der Periode $2 π$ .

Graphen von trigonometrischen Funktionen

#Trigonometrie #Amplitude #Periode #Sinus #Kosinus #Einheitskreis #Sinusfunktion #Kosinusfunktion #Cosinus #cosinusfunktion #periodische Funktion #Sinuskurve #Winkelfunktion

Definition: Eine Funktion f heißt periodisch, wenn es eine Zahl a≠0 gibt, sodass für alle $x, x + a \in D_{f}$ gilt:
$f (x + a) = f (x)$ .
Die kleinste positive Zahl p mit dieser Eigenschaft nennt man Periode.

Anmerkung: Mit $f (x + a) = f (x)$ gilt auch $f (x) = f (x + k \cdot a)$ , sofern nur die Werte $x + k \cdot a ($ mit $k \in ℤ)$ zum Definitionsbereich gehören.

Die Graphen periodischer Funktionen sind verschiebungssymmetrisch, sie gehen durch Verschiebung längs der x-Achse mit einer Verschiebungsweite p oder $k \cdot p$ in sich über.

Beispiel einer periodischen Funktion

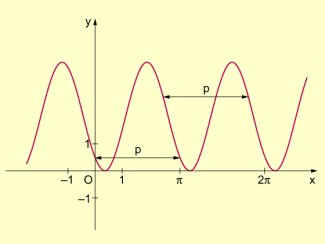
Die bekanntesten periodischen Funktionen sind die trigonometrischen Funktionen. Die Sinusfunktion und die Kosinusfunktion sind periodisch mit der Periode $2 π$ . Aus ihnen lassen sich weitere periodische Funktionen zusammensetzen, z.B. die Funktionen $f (x) = a \cdot \sin b x$ mit der Periode $p = \frac{2 π}{b}$ .

Beispiel 1: Die Periode der Funktion $f (x) = 3 \sin \frac{1}{4} (x + π)$ ist zu bestimmen.

Die Funktion ist vom Typ $f (x) = a \cdot \sin b (x + c)$ . Für die Periode von f gilt allgemein $p = \frac{2 π}{b}$ . Damit hat f die Periode $p = 8 π$ .

Beispiel 2: Die Funktion $f (x) = 2 \sin (2 (x + 2)) + 2$ ist zu skizzieren.

Der Graph dieser Funktion f geht aus dem Graphen der Sinusfunktion durch folgende Modifikationen hervor:

Streckung in Richtung der y-Achse mit dem Faktor 2;
Streckung in Richtung der x-Achse mit dem Faktor $\frac{1}{2}$ (Stauchung);
Verschiebung um zwei Einheiten in Richtung der x-Achse nach links;
Verschiebung um zwei Einheiten in Richtung der y-Achse nach oben

Für die Periode p gilt $p = \frac{2 π}{2} = π$ .
Abschließend soll noch eine Aussage für zusammengesetzte Funktionen der Form $f (x) = a_{1} \cdot \sin b_{1} x + a_{2} \cdot \sin b_{2} x$ gemacht werden.
Diese sind periodisch, wenn $b_{1}$ und $b 2$ in einem ganzzahligen Verhältnis zueinander stehen, d.h., wenn $b_{1} : b_{2} = m : n$ gilt und m und n teilerfremde ganze Zahlen sind.
Die Periode des ersten Summanden ist dann $\frac{2 π}{b_{1}}$ , die des zweiten $\frac{2 π}{b_{2}}$ , und es gilt:
$\frac{2 π}{b_{1}} : \frac{2 π}{b_{2}} = b_{2} : b_{1} = n : m$
Das heißt, n Perioden des ersten Summanden entsprechen genau m Perioden des zweiten. Deshalb hat die Gesamtfunktion die Periode $m \cdot \frac{2 π}{b_{1}} = n \cdot \frac{2 π}{b_{2}}$ .

Beispiel 3: Die Periode der Funktion $f (x) = \sin 3 x + 2 \sin \frac{2}{3} x$ ist zu bestimmen.

Die Perioden der Einzelfunktion obiger zusammengesetzter Funktion sind $\frac{2}{3} π$ bzw. $3 π$ , ihr Verhältnis ist $\frac{2}{3} π : 3 π = 2 : 9$ , die Periode der betrachteten Funktion ist demzufolge $9 \cdot \frac{2}{3} π = 2 \cdot 3 π = 6 π$ .

Mathe Note verbessern?

Kostenlos bei Duden Learnattack registrieren und ALLES 48 Stunden testen.

Kein Vertrag. Keine Kosten.

40.000 Lern-Inhalte in Mathe, Deutsch und 7 weiteren Fächern
Hausaufgabenhilfe per WhatsApp
Original Klassenarbeiten mit Lösungen
Deine eigene Lern-Statistik
Kostenfreie Basismitgliedschaft

Mathe kostenlos lernen

Verwandte Artikel

Periodizität von Funktionen

Graphen von trigonometrischen Funktionen

Rechtliches

Einloggen