Standardnormalverteilung
Eine Normalverteilung wird vollständig bestimmt durch ihren Erwartungswert und ihre Streuung . Es liegt deshalb die Frage nahe, ob man eine beliebige Normalverteilung in eine spezielle Normalverteilung transformieren kann – und zwar in eine mit solchen Parametern, die den Termen ihrer Dichte- und Verteilungsfunktion eine möglichst einfache Gestalt geben. Für eine Zufallsgröße wäre dies der Fall:
Für die Werte erhält man als Spezialfall die Standardnormalverteilung.
Ist X eine normalverteilte Zufallsgröße mit den Parametern und , dann ist die standardisierte Zufallsgröße ebenfalls normalverteilt, und zwar . Man nennt diese Zufallsgröße dann standardnormalverteilt und spricht von der Standardnormalverteilung.
Die Dichtefunktion der Standardnormalverteilung bezeichnet man mit . Es gilt:
-
Dichtefunktion der Standardnormalverteilung
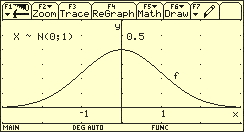
Der Graph dieser Dichtefunktion, die sogenannte gaußsche Glockenkurve, ist axialsymmetrisch zur y-Achse, weil für alle gilt.
Für hat der Graph ein Maximum mit dem Wert .
Die beiden Wendepunkte liegen bei und .
Die Verteilungsfunktion der Standardnormalverteilung wird mit bezeichnet und häufig auch gaußsche Summenfunktion genannt. Es gilt:
Der Graph dieser Verteilungsfunktion ist punktsymmetrisch zum Symmetriezentrum (0; 0,5), weil für alle gilt.
-
Verteilungsfunktion der Standardnormalverteilung
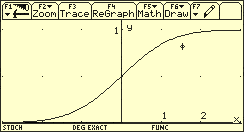
Es sei Y standardnormalverteilt.
Dann kann man die Wahrscheinlichkeit
sowohl als Inhalt der Fläche unterhalb des Graphen der Dichtefunktion über dem Intervall als auch als Wert der Verteilungsfunktion an der Stelle x = a interpretieren.
Es gelten folgende Rechenregeln für die Wahrscheinlichkeiten :
Es sei nun und , d.h., es ist .
Für eine solche Zufallsgröße X lauten diese Rechenregeln (unter Beachtung der Transformationsgleichung ) dann wie folgt:
Mit der Rückführung einer beliebigen Normalverteilung auf die Standardnormalverteilung reduziert sich der Aufwand zur Berechnung der entsprechenden Wahrscheinlichkeiten erheblich. Trotzdem bleibt die Schwierigkeit bestehen, dass die Dichtefunktion keine elementare Stammfunktion besitzt.
Man hat deshalb die Verteilungsfunktion der Standardnormalverteilung (und auch die Dichtefunktion ) tabelliert, und zwar nur für nichtnegative Argumente, da die Funktionswerte für negative Argumente durch die Gleichung gewonnen werden können. Dabei wurden die Funktionswerte von mithilfe folgender Reihendarstellung von bestimmt:
Auf dem (Taschen-)Computer kann man dieses Verfahren nachvollziehen, indem die n-te Partialsumme dieser Reihe als Funktionsterm in Abhängigkeit von x und n definiert wird.
![]()
Moderne Mathematiksoftware verfügt über spezielle Programme zur Integralberechnung, sodass es möglich ist, die Werte von
direkt zu bestimmen. Dabei wird aber mitunter eine erhebliche Rechenzeit benötigt, die vor allem aus der unteren Integrationsgrenze resultiert.
Die Rechenzeit kann erheblich verkürzt werden, wenn man als untere Integrationsgrenze eine endliche Zahl wählt (etwa –5).
![]()
Das führt im Allgemeinen zu keinem Genauigkeitsverlust, denn es gilt z.B.:
Der Anwender benötigt also bei der Arbeit mit der Normalverteilung keine Integralrechnung, sondern nur ein Tafelwerk der Stochastik oder einen entsprechenden Computer.

