Unterräume und Erzeugendensysteme
Die Betrachtung der Bedingungen der Vektorraumdefinition führen zur Definition eines Unterraumes sowie dem Unterraumkriterium und weiter zum Begriff des Erzeugendensystems. Es werden Beispiele von Unterräumen spezieller Vektorräume angeführt.
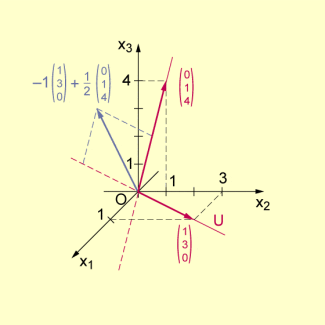
Durch Beschreibung der Vektoren des Anschauungsraumes mittels Koordinaten erhält man den Vektorraum V mit
In U werden die Ortsvektoren der Punkte einer Ebene durch den Ursprung O zusammengefasst, beispielsweise:
Die Teilmenge U des Vektorraumes V ist bezüglich der Addition und der skalaren Vervielfachung in V wieder ein Vektorraum.
-
Unterraum U von Ortsvektoren; Ebene enthält O
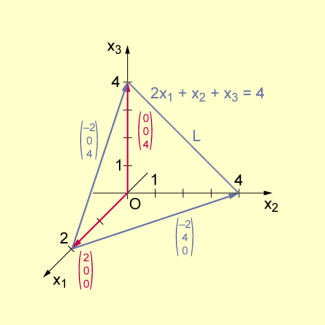
Beziehen sich dagegen die Ortsvektoren auf Punkte einer Ebene, die nicht den Ursprung O enthält, wie in der Menge
so ist die Teilmenge L von V kein Vektorraum, da (und es gibt viele Begründungen dafür( z.B. , aber , was der Eigenschaft (4) der Vektorraumdefinition widerspricht.
-
Unterraum L von Ortsvektoren; Ebene enthält nicht O
- Definition: Eine Teilmenge U eines Vektorraumes V, die selbst bezüglich der Addition und der Vervielfachung in V ein Vektorraum ist, heißt Unterraum U des Vektorraumes V.
Ist eine Teilmenge U eines Vektorraumes selbst bezüglich ein Vektorraum, so führen die Summenbildung und die skalare Vervielfachung nicht aus U hinaus und es existieren ein Nullelement und für jedes Element ein entgegengesetztes Element in U. Die restlichen Bedingungen der Vektorraumdefinition gelten auf ganz V und damit auch in U.
Daraus ergibt sich der folgende Satz:
- Satz (Unterraumkriterium): Eine nichtleere Teilmenge U eines Vektorraumes V ist genau dann ein Unterraum von V, wenn für alle Vektoren aus U und für alle reellen Zahlen r gilt:
Beweis:
Die Bedingungen sind notwendig. Sie sind auch hinreichend, da nach der vorbereitenden Bemerkung zum Satz für eine Teilmenge U mit den beiden Bedingungen nur noch (3) und (4) aus der Vektorraumdefinition nachzuweisen sind:
Im Vektorraum V ist der Nullvektor: Er gehört auch zu U, da ist, und folglich gilt (3) in U.
Wegen ist mit stets , was (4) in U bestätigt.
w.z.b.w.
Beispiele von Unterräumen spezieller Vektorräume
(1) Für jede natürliche Zahl n ist der Vektorraum der Polynome höchstens n-ten Grades (definiert sind alle Polynome auf ganz ) jeweils ein Unterraum des Funktionsraumes aller Funktionen mit Definitionsbereich .
(2) Im einleitend betrachteten Vektorraum V der Ortsvektoren des Anschauungsraum bilden Unterräume:
- der Vektorraum, der nur aus dem Nullvektor besteht;
- alle Ortsvektoren, die Punkte einer festen Geraden g durch O beschreiben;
- alle Ortsvektoren, die Punkte einer festen Ebene durch O beschreiben;
- der ganze Vektorraum V.
Der einleitend angegebene Unterraum U von V wird durch alle Linearkombinationen der Vektoren
gebildet; die Koordinaten der Vektoren
von U
genügen der Beziehung .
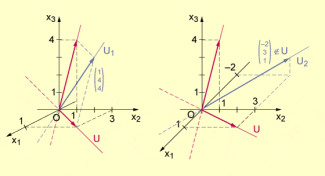
Es ist mit
ein Unterraum von U und damit auch von V (vergleiche linke Figur in der folgenden Abbildung).
Der Unterraum von V mit
ist aber kein Unterraum von U (vergleiche rechte Figur in der folgenden Abbildung).
-
Beispiel und Gegenbeispiel für einen Unterraum von U
(3) Die Lösungsmenge eines homogenen linearen Gleichungssystems mit n Variablen ist ein Unterraum des Vektorraumes aller n-Tupel reeller Zahlen.
Linearkombinationen und Erzeugendensysteme
Gegeben seien ein Vektorraum V und die Vektoren .
Wir betrachten die Menge M aller Linearkombinationen dieser Vektoren, d.h. die Menge M mit
Diese Menge hat bezüglich der Addition und der Vervielfachung in V die folgenden Eigenschaften:
Das heißt, M ist ein Unterraum von V, und es gilt der folgende Satz:
- Satz: Sind Vektoren eines Vektorraumes V, so ist die Menge aller Linearkombinationen dieser Vektoren bezüglich der Addition und der Vervielfachung in V wieder ein Vektorraum, d.h. ein Unterraum von V.
Für so erzeugte Unterräume sind die in der folgenden Definition angegebenen Benennungen üblich:
- Definition: Der durch alle Linearkombinationen der Vektoren gebildete Unterraum U eines Vektorraumes heißt die lineare Hülle U der Vektoren (bzw. der von erzeugte Unterraum U bzw. der von aufgespannte Unterraum U).
Die Menge wird ein Erzeugendensystem des Unterraumes U genannt.
Wir betrachten dazu das folgende Beispiel.
- Beispiel: Es sei der Vektorraum der Polynome höchstens 5. Grades, also
Die Polynome mit
gehören zu .
Bildet man die Menge M aller Linearkombinationen dieser vier Polynome und wählt dabei die variablen Koeffizienten passend zu den Exponenten von x, so kann M wie folgt notiert werden:
Aus folgt . Damit ist M nach dem Unterraumkriterium ein Unterraum von , der durch aufgespannt wird.
Man erkennt, dass schon die drei Polynome den Unterraum M aufspannen und dass ein minimales Erzeugendensystem des Unterraumes M ist.

