Drachenviereck
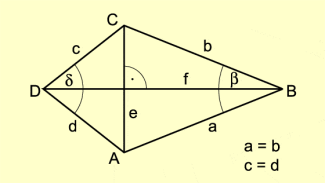
Ein Drachenviereck ist ein Viereck, in dem jeweils die beiden Seiten gleich lang sind, die einen Eckpunkt auf der Symmetrieachse gemeinsam haben (Bild 1). Die Diagonalen stehen in einem (gleichschenkligen) Drachenviereck senkrecht aufeinander. Eine von ihnen ist die Symmetrieachse.
Diese Diagonale halbiert die andere Diagonale und die entsprechenden Innenwinkel des Drachenvierecks.
Drachenviereck
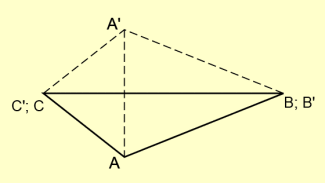
Spiegelt man ein beliebiges Dreieck an einer Dreiecksseite, so entsteht ein Drachenviereck (Bild 2).
Für den Umfang eines Drachenvierecks gilt:
u = a + b + c + d
bzw. mit a = b und c = d
u = 2 (a + c)
Spiegelung eines Dreiecks
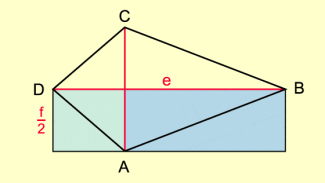
Zerlegt man das Drachenviereck in vier Dreiecke und setzt diese Dreiecke zu einem flächeninhaltsgleichen Rechteck zusammen, so hat das Rechteck den Flächeninhalt (Bild 3).
Für den Flächeninhalt eines Drachenvierecks gilt:
Zerlegung eines Drachenvierecks
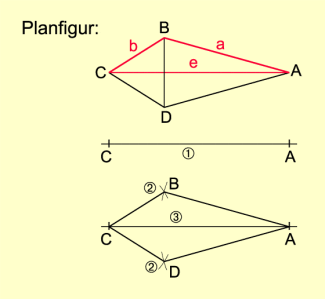
Die Konstruktion eines Drachenvierecks ist bereits mit drei voneinander unabhängigen Angaben möglich (Bild 4).
Beispiel:
Gegeben sind die beiden Seiten a bzw. b und die Diagonale e.
- Auf einer Geraden wird die Strecke CA mit abgetragen.
- Um A wird ein Kreisbogen mit dem Radius a gezeichnet. Um C wird ein Kreisbogen mit dem Radius b gezeichnet.
- Die Schnittpunkte der beiden Kreisbogen sind B und D. Die Punkte B und D werden mit A und C verbunden.
Konstruktion eines Drachenvierecks
Flächeninhalt Viereck Konstruktion interaktiv Mathcad Symmetrieachse Umfang Diagonalen Drachenviereck Rechenbeispiel Berechnungsbeispiel
Stand: 2010
Dieser Text befindet sich in redaktioneller Bearbeitung.
Ein Angebot von 