Kollineare Punkte
Die Kollinearität beschreibt die Lagebeziehungen mehrerer Punkte.
Zwei Punkte sind stets kollinear, da sie eindeutig eine Gerade festlegen – die Verbindungsgerade. Drei und mehr Punkte heißen kollinear genau dann, wenn sie auf ein und derselben Geraden liegen.
Somit sind alle Punkte, die in einer Geraden enthalten sind, kollinear.
Die Verbindungsstrecken dreier nicht kollinearer Punkte bilden ein Dreieck.
Die Kollinearität beschreibt die Lagebeziehungen mehrerer Punkte.
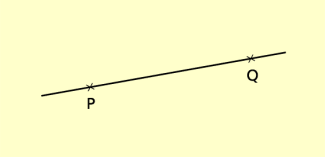
Zwei Punkte sind stets kollinear, da sie eindeutig eine Gerade festlegen – die Verbindungsgerade (Bild 1).
Drei und mehr Punkte heißen kollinear genau dann, wenn sie auf ein und derselben Geraden liegen.
Somit sind alle Punkte, die in einer Geraden enthalten sind, kollinear.
Die Verbindungsstrecken dreier nicht kollinearer Punkte bilden ein Dreieck.
Lagebeziehungen mehrerer kolineare Punkte werden mit der Relation „... liegt zwischen ... und ...“ (Zwischenrelation) näher charakterisiert. Diese Relation wird als Grundrelation entsprechend unserer Anschauung benutzt, also nicht definiert.
-
Verbindungsgerade zweier Punkte
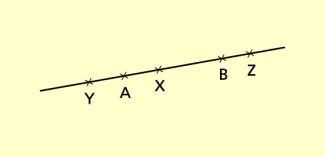
Folgende Eigenschaften der Relation werden im Einklang mit der Erfahrung als gegeben in Axiomen vorausgesetzt (Bild 2):
- Von drei verschiedenen Punkten einer Geraden liegt genau ein Punkt zwischen den beiden anderen.
- Zwischen zwei Punkten A und B einer Geraden gibt es stets mindestens einen weiteren Punkt X der Geraden.
- Außerdem gibt es Punkte Y und Z auf der Geraden, sodass A zwischen Y und B liegt und dass B zwischen A und Z liegt.
Sind vier Punkte nicht kollinear bedeutet das, dass jeweils nicht je drei von ihnen auf einer Geraden liegen oder nicht mehr als zwei Punkte eine gemeinsame Gerade haben dürfen. Es gibt dann sechs Verbindungsstrecken. Sind fünf Punkte nicht kollinear, so gibt es zehn Verbindungsstrecken. Allgemein gilt:
Die Anzahl der Verbindungsstrecken von n nicht kollinearen Punkten beträgt:
-
Lagebeziehung mehrerer kollinearer Punkte