Komplementwinkelbeziehungen

Beziehungen zwischen den Sinus- und Kosinuswerten von Komplementwinkeln werden Komplementwinkelbeziehungen genannt. Vergleicht man die Graphen der Sinusfunktion und der Kosinusfunktion, so liegt die Vermutung nahe, dass sie gegeneinander um $\frac{π}{2}$ in Richtung der Abszissenachse verschoben sind.

Beziehungen zwischen den Sinus- und Kosinuswerten von Komplementwinkeln werden Komplementwinkelbeziehungen genannt.
Vergleicht man die Graphen der Sinusfunktion und der Kosinusfunktion (Bild 1), so liegt die Vermutung nahe, dass sie gegeneinander um $\frac{π}{2}$ in Richtung der Abszissenachse verschoben sind und dass
$\sin x = \cos (\frac{π}{2} - x) b z w . \cos x = \sin (\frac{π}{2} - x)$
gilt.

Funktionsgraphen der Sinus- und Kosinusfunktion

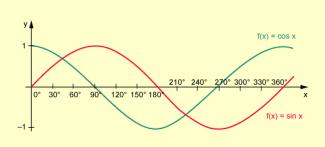
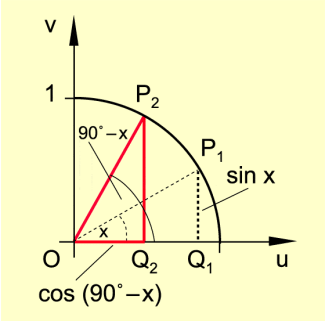
Bild 2 verdeutlicht für Winkel x mit $0 ° < x < 90 °$ , dass diese Komplementwinkelbeziehung tatsächlich zutrifft.
Der Beweis lässt sich über die Kongruenz der Dreiecke ${OQ}_{1} P_{1} und {OQ}_{2} P_{2}$ führen.

Komplementwinkelbeziehung

Stand: 2010
Dieser Text befindet sich in redaktioneller Bearbeitung.

Mathe Note verbessern?

Kostenlos bei Duden Learnattack registrieren und ALLES 48 Stunden testen.

Kein Vertrag. Keine Kosten.

40.000 Lern-Inhalte in Mathe, Deutsch und 7 weiteren Fächern
Hausaufgabenhilfe per WhatsApp
Original Klassenarbeiten mit Lösungen
Deine eigene Lern-Statistik
Kostenfreie Basismitgliedschaft

Mathe kostenlos lernen

Verwandte Artikel

Komplementwinkelbeziehungen

Rechtliches

Einloggen