Kreiskegel

Werden alle Punkte eines Kreises mit einem Punkt S außerhalb der Kreisebene verbunden, so schließen diese Strecken gemeinsam mit dem Kreis einen Körper ein, der Kreiskegel genannt wird. Er hat einen Kreis als ebene Grundfläche und eine gekrümmte Mantelfläche.

Der Punkt S heißt Spitze des Kreiskegels. Der Abstand der Spitze S von der Grundfläche heißt Höhe. Die Verbindungsstrecken von den Kreispunkten zur Spitze heißen Mantellinien.
Für gerade Kreiskegel gilt:
$s^2=r^2+h^2$

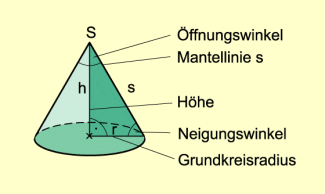
Liegt die Spitze eines Kreiskegels senkrecht über dem Mittelpunkt des Grundkreises, so heißt der Kreiskegel gerade, ansonsten heißt er schief.
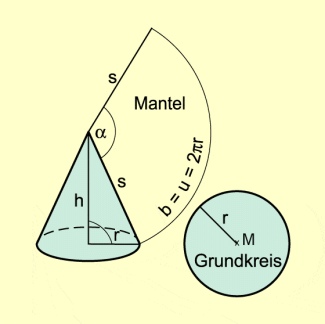
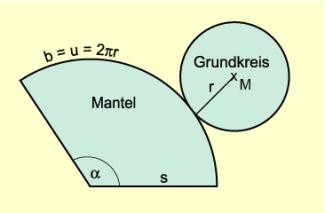
Wird der Kegelmantel längs einer Mantellinie aufgeschnitten und in einer Ebene abgewickelt, so entsteht ein Kreissektor, der zusammen mit der Grundfläche das Netz des Kegels bildet.
Für die Bogenlänge b des durch den Mantel gebildeten Kreissektors mit der Mantellinie s und dem Mittelpunktswinkel (Zentriwinkel) $\alpha$gilt:
$b=2\pi s\cdot \frac{\alpha }{360°}$
Da die Bogenlänge gleich dem Umfang u des Grundkreises des Kegels ist, ergibt sich:
$b=u=2\pi r=2\pi s\cdot \frac{\alpha }{360°}unddamitr=s\cdot \frac{\alpha }{360°}$

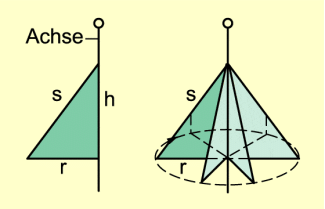
Ein Kegel entsteht, wenn ein rechtwinkliges Dreieck um eine seiner Katheten rotiert. Die Gerade durch diese Kathete heißt Achse des Kegels. Jede Schnittebene durch die Achse ist eine Symmetrieebene des Kegels.

Die Oberfläche $A_O$ eines Kegels setzt sich aus seiner Grundfläche $A_G$und seiner Mantelfläche $A_M$ zusammen. Der Mantel ist ein Kreissektor mit dem Zentriwinkel $\alpha$ und der Mantellinie s als Radius, sodass gilt:
$A_M=\pi s^2\cdot \frac{\alpha }{360°}$
Die Bogenlänge b des Sektors ist gleich dem Umfang u des Grundkreises.
Es gilt :
$r=s\cdot \frac{\alpha }{360°}unddamitfo\lg t{A}_M=\pi rs$
Der Oberflächeninhalt $A_O$ eines geraden Kreiskegels mit dem Grundkreisradius r und der Mantellinie s ist gleich der Summe aus den Inhalten des Grundkreises $A_G$ und der Mantelfläche $A_M$:
$A_G=\pi r^2{A}_M=\pi rs{A}_O=A_G+A_M=\pi r\left(r+s\right)$

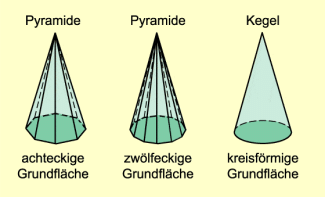
Zur Gewinnung einer Formel für das Kegelvolumen sind die gleichen Überlegungen wie bei der Zylinderformel möglich. Wenn bei einer Pyramide mit einem regelmäßigen n-Eck als Grundfläche die Anzahl der Seiten immer größer wird, nähert sie sich immer mehr der Form eines Kegels an. Die Formel zur Berechnung des Volumens einer Pyramide gilt in analoger Weise auch für einen Kegel.
Das Volumen eines Kreiskegels ist gleich einem Drittel des Produktes aus dem Inhalt der Grundfläche und der Höhe:
$V=\frac{1}{3}\cdot A_G\cdot h=\frac{1}{3}\pi r^{2}h$