Prisma
Ein Körper heißt gerades Prisma, wenn er von zwei zueinander kongruenten und parallelen n-Ecken und von n Rechtecken begrenzt wird. Die n-Ecke heißen Grundfläche und Deckfläche des Prismas. Der Abstand zwischen Grund- und Deckfläche ist die Höhe des Prismas. Der Mantel des Prismas wird von den Seitenflächen gebildet.
Entsprechend der Anzahl der Seitenflächen der Prismen spricht man von dreiseitigen, vierseitigen, fünfseitigen ... Prismen.
Bei geraden Prismen ist die Länge der Höhe gleich der Länge der Seitenkanten, für schiefe Prismen gilt dies nicht.
Der Oberflächeninhalt eines Prismas ergibt sich aus der Summe des doppelten Grundflächeninhalts und des Mantelflächeninhalts.
Für den Inhalt der Mantelfläche des Prismas gilt:
Für den Oberflächeninhalt des Prismas gilt:
Prisma - Beispiel Oberflächeninhalt anhand Tetrapacks
B. Mahler, Fotograf, Berlin
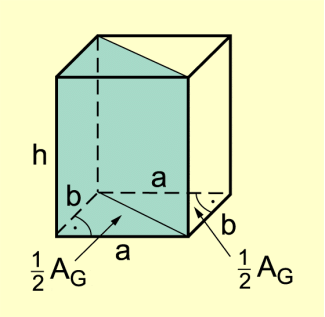
Die Formel für die Berechnung des Volumens eines Prismas lässt sich aus der Volumenformel für einen Quader ableiten. Für das Volumen eines Quaders gilt:
(mit c = h)
Durch einen senkrechten Schnitt kann der Quader in zwei zueinander kongruente Prismen mit rechtwinkligen Dreiecken als Grundfläche zerlegt werden. Für das Volumen jedes der beiden Teilprismen gilt:
entspricht der Grundfläche des Teilprismas, die ein rechtwinkliges Dreieck ist. Also gilt auch für jedes Prisma mit einem rechtwinkligen Dreieck als Grundfläche:
Weil sich jedes Vieleck vollständig in rechtwinklige Dreiecke zerlegen lässt, kann auch jedes Prisma vollständig in Teilprismen zerlegt werden, die sämtlich rechtwinklige Dreiecke als Grundfläche und die gleiche Höhe h haben. Für das Volumen jedes beliebigen Prismas mit der Grundfläche und der Höhe h gilt:
Prismazerlegung
interaktiv Mathcad Höhe Rechenbeispiel Grundfläche Mantel Oberflächeninhalt Volumen Berechnungsbeispiel Prisma Deckfläche Mantelflächeninhalt
Stand: 2010
Dieser Text befindet sich in redaktioneller Bearbeitung.
Ein Angebot von 