Kreiszylinder
Einen Körper mit zwei zueinander kongruenten und parallelen Kreisen als Grund- und Deckfläche nennt man Kreiszylinder. Liegen die Mittelpunkte der Kreisflächen des Zylinders senkrecht übereinander, so handelt es sich um einen geraden Kreiszylinder. Man kann sich einen geraden Kreiszylinder auch durch Rotation eines Rechtecks um eine seiner Seiten entstanden vorstellen.
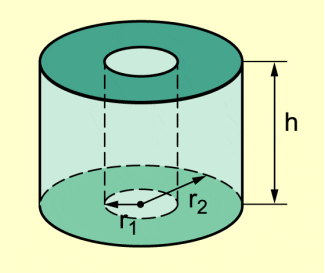
Die Mantelfläche eines geraden Kreiszylinders lässt sich abwickeln, d. h. in eine Ebene ausbreiten. Die Mantelfläche ist ein Rechteck mit den Kantenlängen h (Höhe des Kreiszylinders) und u (Umfang der Grundfläche).
Der Oberflächeninhalt eines geraden Kreiszylinders ist die Summe aus dem doppelten Flächeninhalt der Grundfläche und dem Flächeninhalt des Mantels:
Für den Mantelflächeninhalt gilt:
Für den Flächeninhalt der Grundfläche eines Kreiszylinders gilt:
Netz eines Zylinders
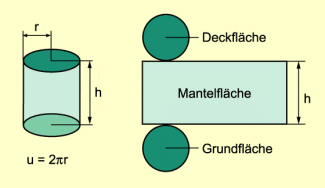
Vergrößert man bei einem Prisma mit einem regelmäßigen n-Eck als Grundfläche die Anzahl der Seitenflächen, so nähert es sich immer mehr der Form eines Zylinders an. Das Volumen eines Kreiszylinders kann daher nach der Formel für die Berechnung des Prismenvolumens berechnet werden:
Volumen eines Zylinders
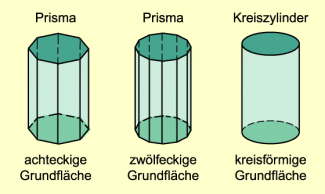
Schneidet man aus einem Kreiszylinder einen zur Achse symmetrischen kleineren Kreiszylinder gleicher Höhe aus, so entsteht ein Hohlzylinder. Für den Oberflächeninhalt eines Hohlzylinders gilt:
Die Formel für das Volumen eines Hohlzylinders lässt sich sowohl aus der Differenz der Volumina der beiden Zylinder als auch über die Flächeninhaltsformel für Kreisringe ableiten:
Hohlzylinder
interaktiv Mathcad Hohlzylinder Rechenbeispiel Kreiszylinder Oberflächeninhalt Volumen Berechnungsbeispiel Mantelfläche
Stand: 2010
Dieser Text befindet sich in redaktioneller Bearbeitung.
Ein Angebot von 