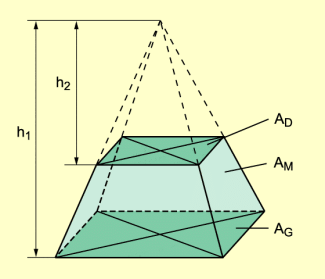
Pyramidenstumpf
Wird eine Pyramide durch eine zur Grundfläche der Pyramide parallele Ebene geschnitten, so entstehen ein Pyramidenstumpf und die zugehörige Ergänzungspyramide.
Die zueinander parallelen Grund- und Deckflächen des Pyramidenstumpfes haben den Abstand h mit
h = –
( Höhe der Gesamtpyramide, Höhe der Ergänzungspyramide).
Die Grund- und die Deckfläche sind zueinander ähnlich. Für ihre Flächeninhalte gilt:
Der Mantel eines Pyramidenstumpfes ist die Summe der trapezförmigen Seitenflächen. Für den Oberflächeninhalt eines Pyramidenstumpfes gilt:
Das Volumen eines Pyramidenstumpfes ergibt sich aus der Differenz des Volumens der gesamten Pyramide und der Ergänzungspyramide. Es gilt:
Schrägbild eines Pyramidenstumpfs
Ein Angebot von 