- Lexikon
- Mathematik
- 5 Gleichungen und Ungleichungen
- 5.5 Lineare Ungleichungen
- 5.5.2 Lineare Ungleichungen mit zwei Variablen
- Lineare Ungleichungen, mit zwei Variablen
Lineare Ungleichungen, mit zwei Variablen
Zwei Terme, zwischen denen eines der Zeichen steht, bilden eine Ungleichung.
Ungleichungen der Form oder solche, die durch äquivalentes Umformen in diese Form überführt werden können, heißen lineare Ungleichungen mit zwei Variablen.
Die Lösungsmenge einer solchen Ungleichung mit zwei Variablen ist ein Menge geordneter Zahlenpaare.
Diese Menge lässt sich grafisch ermitteln, indem man das Ungleichheitszeichen durch ein Gleichheitszeichen ersetzt, die entstandene Gleichung als Funktionsgleichung einer linearen Funktion auffasst und ihren Graphen zeichnet.
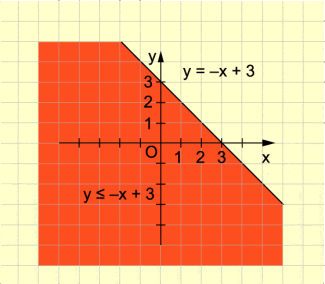
Beispiel 1 (Bild 1):
Es wird der Funktionsgraph und die Lösungsmenge gezeichnet.
Zur Lösungsmenge der Ungleichung gehören die Punkte der Geraden sowie die Punkte unterhalb der Geraden.
Darstellung der Lösungsmenge im Koordinatensystem
Beispiel 2 (Bild 2):
Es wird der Funktionsgraph und die Lösungsmenge gezeichnet.
Zur Lösungsmenge der Ungleichung gehören nicht die Punkte der Geraden, sondern nur die Punkte oberhalb der Geraden.
Darstellung der Lösungsmenge im Koordinatensystem
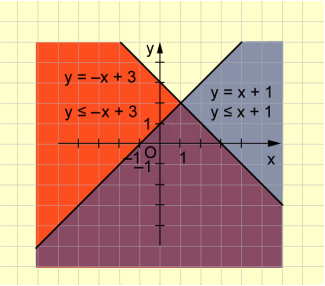
Zwei Ungleichungen mit denselben zwei Variablen bilden ein Ungleichungssystem.
Beispiel 3 (Bild 3):
Die Lösungsmenge eines Ungleichungssystems kann grafisch als Durchschnitt der Lösungsmengen der einzelnen Ungleichungen ermittelt werden.
Darstellung der Lösungsmenge im Koordinatensystem
Funktionsgraph Funktionsgleichung lineare Ungleichungen Ungleichung Ungleichungssystem geordnete Zahlenpaare Lösungsmenge
Stand: 2010
Dieser Text befindet sich in redaktioneller Bearbeitung.
Ein Angebot von 