Logische Operationen

Aus der Umgangssprache ist bekannt, dass einfache Sätze durch Bindewörter zu längeren Satzverbindungen zusammengesetzt werden können. So können Aussagen und Aussageformen verneint oder durch die Wörter „und“, „oder“, „entweder … oder“,
„wenn …, so …“, „genau dann, wenn“ verknüpft werden.
Dabei entsteht eine neue Aussage oder Aussageform als Verbindung zweier anderer Aussagen oder Aussageformen.

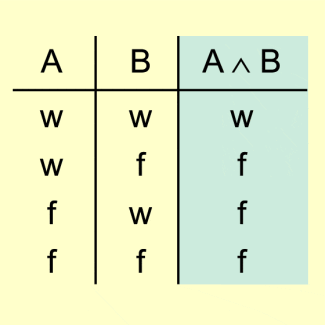
UND-Verknüpfung (Konjunktion) zweier Aussagen A und B

Die Konjunktion „A und B“ $\left(\text{A}\wedge \text{B}\right)$ ist genau dann wahr, wenn die Teilaussagen A und B zugleich wahr sind (Bild 1).

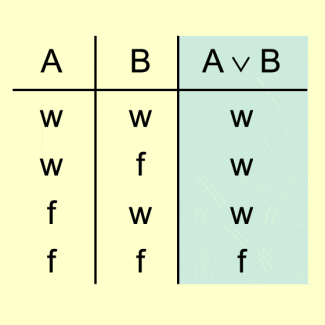
ODER -Verknüpfung (Disjunktion) zweier Aussagen A und B

Die Disjunktion „A oder B“ $\left(\text{A}\vee \text{B}\right)$ ist genau dann wahr, wenn mindestens eine der Teilaussagen A bzw. B wahr ist (Bild 2).

ENTWEDER- ODER - Verknüpfung (Alternative) zweier Aussagen A und B

Die Alternative „entweder A oder B“ $\left(\text{A}\vee \text{B}\right)$ ist genau dann wahr, wenn e ine der beiden Teilaussagen wahr und zugleich die andere falsch ist.
In dieser Weise wird das Wort „oder“ in der Umgangssprache benutzt.

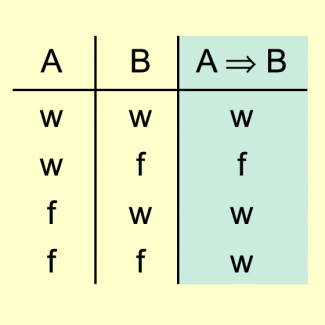
WENN-DANN-Verknüpfung (Implikation) zweier Aussagen A und B

Die Implikation „wenn A, dann B“ $\left(\text{A}\Rightarrow \text{B}\right)$ ist genau dann falsch, wenn A (Voraussetzung oder auch Prämisse genannt) wahr und gleichzeitig B (Schlussfolgerung oder auch Konklusion genannt) falsch ist.
In allen anderen Fällen ist die Aussage „wenn A, dann B“ wahr (Bild 3).

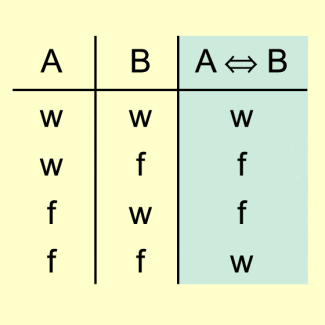
GENAU DANN-WENN-Verknüpfung (Äquivalenz) zweier Aussagen A und B

Die Äquivalenz „A genau dann, wenn B“ $\left(\text{A}\iff \text{B}\right)$ ist genau dann wahr, wenn beide Aussagen den gleichen Wahrheitswert haben (Bild 4).

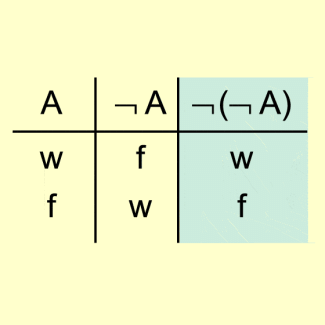
Verneinung (Negation) einer Aussage

Die Aussage A und ihre Negation „nicht A“ ( $\neg \text{A}$) haben entgegengesetzte Wahrheitswerte.
Entsprechend hat die Negation der Negation einer Aussage den gleichen Wahrheitswert wie die Aussage selbst (Bild 5).

Beispiel:
Aussage A: Es regnet.
Negation von A: Es regnet nicht.
Negation der Negation: Es stimmt nicht, dass es nicht regnet.

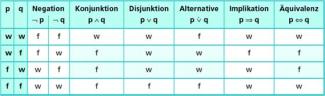
Wahrheitswerteverlauf zusammengesetzter Aussageformen

Wie Aussagen können auch Aussageformen verknüpft werden. Da Aussageformen freie Variablen enthalten, kann ihnen kein Wahrheitswert zugeordnet werden. Erst nach einer Variablenbelegung entstehen wahre oder falsche Aussagen.
Die nebenstehende Tabelle (Bild 6) zeigt den Wahrheitswerteverlauf zusammengesetzter Aussageformen je nach dem, ob die Aussageformen p und q zu wahren oder falschen Aussagen werden.