Mengen, Darstellung

Mengen lassen sich in beschreibender oder in aufzählender Form angeben.
Ist x ein Element der Menge M, so schreibt man $\text{x}\in \text{M}$.
Ist x kein Element der Menge M, so schreibt man $\text{x}\notin \text{M}$.

Alle Elemente der Menge werden angeben, z. B. in geschweiften Klammern aufgeschrieben.
Beispiel:
Menge der möglichen Augenzahlen eines
Würfels$\text{M}=\left\{\text{1;}\text{2;}\text{3;}\text{4;}\text{5;}\text{6}\right\}$

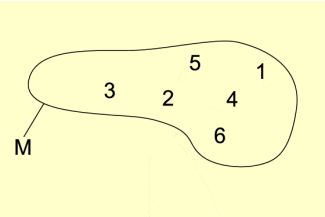
Alle Elemente der Menge werden in ein Diagramm eingetragen. Solche Diagramme werden nach dem englischen Logiker JOHN VENN (1834 bis 1923) auch VENN-Diagramme genannt.

Der Grundbereich und die mengenbildende Eigenschaft werden in Worten beschrieben.
Beispiel:
M ist die Menge aller natürlichen Zahlen, die kleiner
als 20 und durch 5 teilbar sind.

Der Grundbereich und die mengenbildende Eigenschaft (die eine Aussageform ist) werden als Zeichenreihe in einer geschweiften Klammer angegeben.
Beispiel:
$\text{M}=\left\{\text{x}\in \mathbb{N}\text{:}\text{x}<\text{20}\wedge 5|\text{x}\right\}$
Gesprochen: M ist die Menge aller Elemente x aus $\mathbb{N}$, für die gilt:
x ist kleiner als 20 und 5 teilt x.