Parkettierung

Unter Parkettierung versteht man das lückenlose Auslegen einer Fläche mit Figuren.
Ein Parkettfußboden besteht aus einer regelmäßigen Anordnung rechteckiger Holzbretter und ergibt ein schönes Muster.

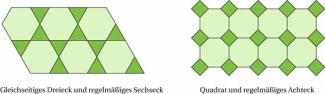
Treten die Muster regelmäßig auf, so spricht man von einer regulären Parkettierung. Die einfachsten Formen für Parkettierung erhält man, wenn man regelmäßige Vielecke aneinanderlegt. Für das gleichseitige Dreieck, das Quadrat und das regelmäßige Sechseck ist es ganz einfach.

Legt man regelmäßige Fünfecke aneinander, so bleiben Lücken, die selbst wieder neue Figuren bilden. Nun kann man weiter versuchen, verschiedene n-Ecke miteinander so zu kombinieren, dass keine Lücken entstehen.

Die Darstellung regelmäßiger, symmetrischer Bilder spielt z. B. in der islamischen Kultur eine große Rolle. Da es nicht gestattet war, menschliche Abbilder zu schaffen, wurden die Gebäude mit schönen Ornamenten und Parkettierungen geschmückt. Zu den aufwendigsten gestalteten Bauwerken gehört die von den Mauren erbaute Burg bei Grenada in Spanien.

In Europa interessierten sich zuerst die Wissenschaftler für die regelmäßigen Muster. Mathematiker untersuchten die geometrischen Strukturen und die Kristallografen fanden heraus, dass sich viele Muster in der Natur z. B. bei Gesteinen und Kristallen finden lassen.

Auch Künstler wie der berühmte holländische Grafiker MAURITS CORNELIS ESCHER (1898 bis 1972) waren von der Schönheit dieser Parkettierungen begeistert. Sie entwickelten Grafiken, in denen sie abstrakte Figuren durch Vögel, Reiter, Eidechsen und sogar durch räumliche Gegenstände ersetzten.