Quadrantenbeziehungen

Für Winkel x mit $\frac{\pi }{2}<\text{x}<2\pi$ lassen sich aufgrund der Definitionen der Sinus-, der Kosinus- und der Tangensfunktion Zusammenhänge zwischen den Werten dieser Funktionen aus dem I. und dem II. bis IV. Quadranten ableiten.
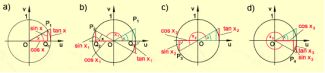
Wir betrachten dazu die im Bild 1 dargestellten Sachverhalte:
Wir bezeichnen in Fig. b den Winkel mit $\sphericalangle {\text{ Q}}_{\text{2}}{\text{OP}}_{\text{2}}$.
Dann ist $x_1=180°-x$ (in Bogenmaß $x_1=\pi -x$).
Die Figuren a und b lassen dann vermuten, dass es zwischen den Sinuswerten von x und $x_1$ (im I. bzw. II. Quadranten) einen Zusammenhang gibt, dass nämlich $\sin \left(\pi -x\right)=\sin x$ gilt. Wir überprüfen diese Vermutung:
$\begin{array}{l}\left(1\right)\left|\overrightarrow{O{P}_1}\right|=\left|\overrightarrow{O{P}_2}\right|\\ \left(2\right)\sphericalangle P_{1}O{Q}_1=\sphericalangle Q_{2}O{P}_2=x\\ \left(3\right)\sphericalangle O{Q}_1{P}_1=\sphericalangle P_2{Q}_{2}O=90°\end{array}$
Aus den Voraussetzungen
folgt nach dem Kongruenzsatz wsw
$\Delta O{Q}_1{P}_1\cong \Delta O{P}_2{Q}_{2}unddamit\left|\overrightarrow{O{P}_1}\right|=\left|\overrightarrow{O{P}_2}\right|.$

Wegen $\left|\overrightarrow{O{P}_1}\right|=\sin xund\left|\overrightarrow{O{P}_2}\right|=\sin x_1=\sin \left(\pi -x\right)$ ergibt sich daraus aber die vermutete Beziehung $\sin \left(\pi -x\right)=\sin x$.

In entsprechender Weise lassen sich unter Verwendung von Fig. b bis d die folgenden „Quadrantenbeziehungen“ ableiten:
$\begin{array}{l}\cos \left(\pi -x\right)=-\cos x\sin \left(\pi +x\right)=-\sin x\sin \left(2\pi -x\right)=-\sin x\\ \tan \left(\pi -x\right)=-\tan x\cos \left(\pi +x\right)=-\cos x\cos \left(2\pi -x\right)=\cos x\\ \tan \left(\pi +x\right)=\tan x\tan \left(2\pi -x\right)=-\tan x\end{array}$

Zusammenfassung:
Unter Einbeziehung des Zusammenhangs 

$\tan x=\frac{1}{\cot x}$ erhalten wir: