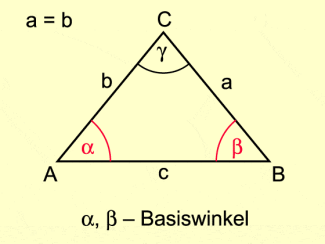
Sätze über Dreiecke
Zwischen den Winkeln und Seiten in einem Dreieck gelten zahlreiche Zusammenhänge.
So besteht zwischen den Winkeln eines Dreiecks folgende Beziehung:
Die Summe der Innenwinkel eines Dreiecks beträgt 180° (Innenwinkelsummensatz).
Für die Seiten eines Dreiecks gilt folgende Beziehung:
Die Summe der Längen zweier Seiten ist stets größer als die Länge der dritten Seite (Dreiecksungleichung).
Zwischen den Seiten und Winkeln in einem Dreieck gilt folgende Beziehung:
Der längeren von zwei Seiten liegt stets der größere der entsprechenden Innenwinkel gegenüber.
Zwischen den Winkeln und Seiten in einem Dreieck gelten zahlreiche Beziehungen.
Für die Innenwinkel eines Dreiecks gilt:
Die Summe der Innenwinkel eines Dreiecks beträgt (Innenwinkelsummensatz):
Aus diesem Satz folgt u. a.:
Ein Dreieck hat höchstens einen stumpfen bzw. einen rechten Winkel.
Sind die Größen zweier Winkel gegeben, so lässt sich die Größe des dritten Winkels bestimmen:
-
Dreieck
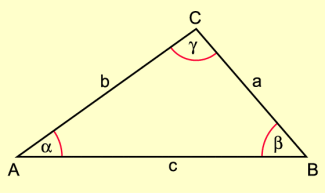
Die Summe von drei zugehörigen Außenwinkeln beträgt .
Jeder Außenwinkel eines Dreiecks ist so groß wie die Summe der beiden nicht anliegenden Innenwinkel (Außenwinkelsatz).
-
Winkel am Dreieck
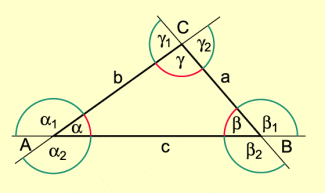
Für die Seiten eines Dreiecks gilt folgende Beziehung:
Die Summe der Längen zweier Seiten ist stets größer als die Länge der dritten Seite (Dreiecksungleichung):
Die Länge einer Seite eines Dreiecks ist damit stets größer als die Differenz aus den Längen der beiden anderen Seiten.
-
Dreiecksungleichung
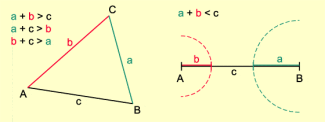
Zwischen den Seiten und Winkeln in einem Dreieck gilt folgende Beziehung:
Der längeren von zwei Seiten liegt stets der größere der entsprechenden Innenwinkel gegenüber:
Aus dieser Beziehung folgt u. a.:
Gleich langen Seiten liegen gleich große Winkel gegenüber. Ein Dreieck mit zwei gleich großen Winkeln hat auch zwei gleich lange Seiten (gleichschenkliges Dreieck). Sind in einem Dreieck alle drei Innenwinkel gleich groß, so sind die drei Seiten gleich lang (gleichseitiges Dreieck). Im rechtwinkligen Dreieck ist die Hypotenuse die längste Seite.