Satz des Pythagoras

Im rechtwinkligen Dreieck ist das Quadrat über der Hypotenuse gleich der Summe der Quadrate über den Katheten:
$a^2+b^2=c^2$
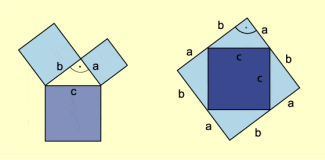
Für diesen Satz sind mehr als 100 Beweise bekannt, von denen der kürzeste wohl der folgende Zerlegungsbeweis ist:
In der Druckversion von Bild 1 kann man sehen, dass sich die gesamte Quadratfläche ${\left(a+b\right)}^2$ aus dem Quadrat $c^2$ und den vier rechtwinkligen Dreiecken mit einer Fläche von $4\cdot \frac{1}{2}\cdot ab=2\cdot ab$zusammensetzt, d. h., es ist:
${\left(a+b\right)}^2=c^2+2\cdot ab$
Damit gilt a² + 2 ·ab + b² = c² + 2 · ab,
woraus a² + b² = c²unmittelbar folgt.

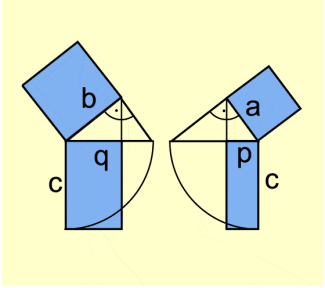
Ein weiterer Beweis erfolgt über die Ähnlichkeit von Dreiecken (Bild 2).
Da im rechtwinkligen Dreieck die durch die Höhe über der Hypotenuse gebildeten Teildreiecke untereinander und dem Gesamtdreieck ähnlich
sind, gilt:
$\frac{q+p}{a}=\frac{a}{p},also{a}^2=p\left(q+p\right)$ bzw. $\frac{q+p}{b}=\frac{b}{p}$, also $b^2=q\left(q+p\right)$
So ergibt sich durch Addition der Beziehungen:
$a^2+b^2=\left(p+q\right)\left(q+p\right)=c\cdot c=c^2$

Es gibt neben den geometrischen Beweisen auch eine Reihe von arithmetischen Beweisen, z. B. den folgenden, für den man den Flächeninhalt des Trapezes berechnen können muss.
Der Beweis erfolgt durch algebraische Umformungen.

Das rechtwinkelige Dreieck ABC (mit Katheten a, b und Hypotenuse c) ist das Grunddreieck. Nun legt man ein kongruentes (deckungsgleiches) Dreieck AED an das Grunddreieck. Verbindet man nun die Eckpunkte E und B, so entsteht ein Trapez DCBE mit den Parallelseiten a und b und der Höhe a + b. Das entstehende Dreieck ABE ist rechtwinklig und gleichschenklig.
Die Dreieck ABC und ADE sind flächeninhaltsgleich, den Flächeninhalt des Trapezes A kann man einerseits als Summe der Flächeninhalte der drei Dreiecke berechnen:
$A=2\cdot A_1+A_2$

Andererseits ist der Flächeninhalt des Trapezes A wie folgt zu berechnen:
Summe der Parallelseiten (= a + b) mal der Höhe (= a + b) dividiert durch 2. Folglich gilt:
$A=\frac{1}{2}\cdot \left(a+b\right)\cdot \left(a+b\right)$
Der Flächeninhalt $A_1$ errechnet sich aus Kathete (a) mal Kathete (b) dividiert durch 2. Der Flächeninhalt $A_2$ des Dreiecks errechnet sich aus Kathete (c) mal Kathete (c) dividiert durch 2.

Fasst man nun alle Erkenntnisse zusammen und betrachtet den Flächeninhalt des Trapezes als Summe der drei Dreiecke, so erhält man folgende Beziehung:
                             $\frac{1}{2}\cdot \left(a+b\right)\cdot \left(a+b\right)=2\cdot \frac{1}{2}\cdot a\cdot b+\frac{1}{2}\cdot c^2$,
woraus man durch Umformungen
                              $a^2+2\cdot ab+b^2=c^2+2\cdot ab$
und schließlich $a^2+b^2=c^2$ erhält.

In seinem 1940 erschienenen Buch „The Pythagorean Proposition“ hat der amerikanische Mathematiklehrer und Collegeprofessor ELISHA SCOTT LOOMIS ca. 370 Beweise zusammengetragen und klassifiziert.

Anwendungen des Satzes des Pythagoras

Mithilfe des Satzes des Pythagoras kann man zu zwei bekannten Seiten eines rechtwinkligen Dreiecks die dritte berechnen. Dies findet bei vielen Berechnungen Anwendung:

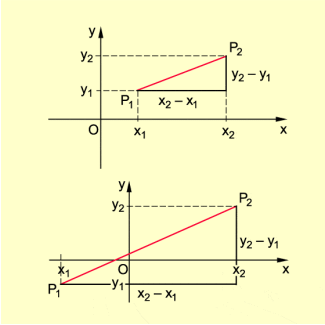
Abstand zweier Punkte in der Ebene und im Raum (Bild 3)

Um den Abstand zweier Punkte in der Ebene anzugeben, betrachte man ein kartesisches Koordinatensystem, indem die Punkte $P_1$ und $P_2$ die Koordinaten $\left(x_1{\text{; y}}_{\text{1}}\right)$ bzw. $\left(x_2{\text{; y}}_{\text{2}}\right)$ haben. In dem rechtwinkligen Dreieck, das aus den Parallelen durch die Punkte zu den Koordinatenachsen gebildet wird, ist der Abstand der Punkte gleich der Länge der Hypotenuse.
Mit dem Satz des Pythagoras erhält man:
$P_1{P}_2=\sqrt{{\left(x_2+x_1\right)}^2+{\left(y_2-y_1\right)}^2}$
Analog ergibt sich für den Abstand zweier Punkte im Raum:
$P_1{P}_2=\sqrt{{\left(x_2+x_1\right)}^2+{\left(y_2-y_1\right)}^2+{\left(z_2-z_1\right)}^2}$

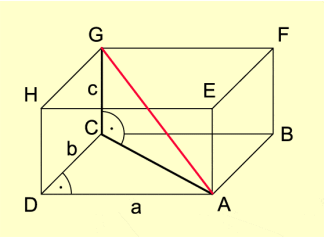
Länge der Raumdiagonale im Quader (Bild 4)

Die Länge der Raumdiagonale ergibt sich aus den Seitenlängen durch zweimalige Anwendung des Satzes des Pythagoras:
$\begin{array}{l}A{C}^2=a^2+b^2\to A{G}^2=A{C}^2+c^2=a^2+b^2+c^2\to \\ AG=\sqrt{a^2+b^2+c^2}\end{array}$

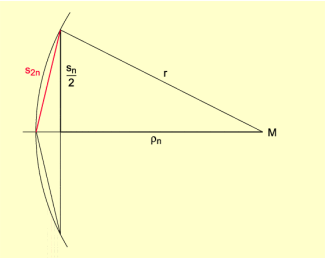
Seitenlänge von regelmäßigen n-Ecken (Bild 5)

Aus der Seitenlänge eines regelmäßigen n-Ecks lässt sich die Seitenlänge des regelmäßigen 2n-Ecks bestimmen:
$\begin{array}{l}{\left(s_{2n}\right)}^2={\left(\frac{s_n}{2}\right)}^2+{\left(r-p_n\right)}^2={\left(\frac{s_n}{2}\right)}^2+{\left(r-\sqrt{r^2-{\left(\frac{s_n}{2}\right)}^2}\right)}^2\\ =2r^2-2r\sqrt{r^2-{\left(\frac{s_n}{2}\right)}^2}\\ s_n=\sqrt{2r^2-r\sqrt{4r^2–s_n{}^2}}\end{array}$

Weiterhin findet der Satz auch bei der Berechnung der Höhe im gleichseitigen Dreieck oder der Raumhöhe in Tetraeder Anwendung.

Praktische Bedeutung hat auch die Umkehrung des Satzes des Pythagoras:
Gilt zwischen den Seiten a, b und c eines Dreiecks die Beziehung
$a^2+b^2=c^2$, dann ist das Dreieck rechtwinklig und hat die Hypotenuse c.
Ganzzahlige Lösungen (a, b, c) der Gleichung $a^2+b^2=c^2$ nennt man auch pythagoreische Zahlen oder pythagoreische Zahlentripel. Die ersten pythagoreischen Zahlentripel (3; 4; 5) und (5; 12; 13) lassen sich durch Probieren finden.
Durch zentrische Streckung mit einem ganzzahligen Streckungsfaktor k entstehen zu den Ausgangsdreiecken ähnliche Dreiecke. Die Tripel (3k; 4k; 5k) bzw. (5k; 12k; 13k) der Seitenlängen dieser Dreiecke sind wieder pythagoreische Zahlentripel.

Verallgemeinerungen des Satzes des Pythagoras

Ähnliche Figuren über den Seiten eines rechtwinkligen Dreiecks

Die Summe der Flächen der Halbkreise über den Katheten eines rechtwinkligen Dreiecks ist gleich der Fläche des Halbkreises über der Hypotenuse (Bild 6).
Beweis:
Aus $a^2+b^2=c^2$ folgt $\frac{1}{2}\pi \cdot a^2+\frac{1}{2}\pi \cdot b^2=\frac{1}{2}\pi \cdot c^2$ durch Multiplikation der Gleichung mit $\frac{1}{2}\pi$, was jeweils die Fläche des Halbkreises beschreibt.

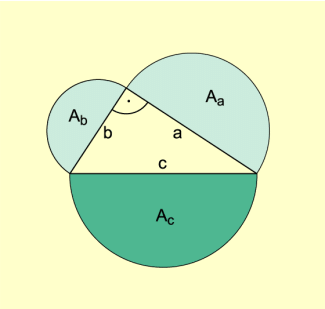
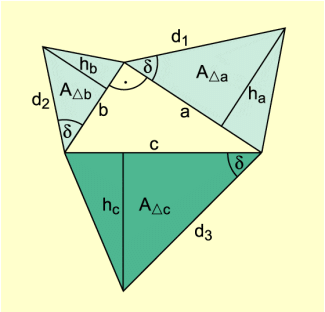
Die Summe der Flächen zueinander ähnlicher Dreiecke über den Katheten eines rechtwinkligen Dreiecks ist gleich der Fläche des zu diesen ähnlichen Dreiecks über der Hypotenuse (Bild 7).
Beweis (nach der Methode des Rückwärtsarbeitens):
Es soll gelten:
$\begin{array}{l}{A}_{\Delta a}+A_{\Delta b}=A_{\Delta c},d.h.\frac{1}{2}a\cdot h_a+\frac{1}{2}b\cdot h_b=\frac{1}{2}c\cdot h_c\text{ oder}\\ \frac{1}{2}a\cdot d_1\cdot \sin \delta +\frac{1}{2}b\cdot d_2\cdot \sin \delta =\frac{1}{2}c\cdot d_3\cdot \sin \delta \text{oder}\\ \text{a}\cdot {\text{d}}_{\text{1}}+b\cdot d_2=c\cdot d_3\text{(*)}\end{array}$
Es gilt:
a : $d_1$= b : $d_2$= c : $d_3$= k
oder
$d_1=k_a,d_2=k_b,d_3=k_c$,
da die Dreiecke ähnlich sind. Nach Einsetzen in (*) folgt:
$a^2+b^2=c^2$

Diese Beziehung lässt sich für beliebige zueinander ähnlich Figuren folgern:
Sind $F_a,F_b,F_c$ zueinander ähnlicher Figuren über den Seiten a, b und c eines rechtwinkligen Dreiecks mit c als Hypotenuse, so gilt für ihre Flächeninhalte:
$A_{Fa}+A_{Fb}=A_{Fc}$