Viereck, allgemein

Eine ebene, von vier Strecken eingeschlossene Figur heißt Viereck.
Die vier Strecken sind die Seiten des Vierecks. Je zwei benachbarte Seiten haben einen Eckpunkt gemeinsam.
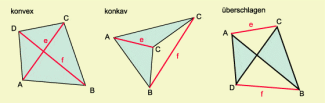
Haben zwei Strecken außer den Endpunkten einen weiteren Punkt gemeinsam, so heißt das Viereck überschlagen.
Ein Viereck heißt konvex, wenn für je zwei Punkte im Inneren des Vierecks auch deren Verbindungsstrecke vollständig im Inneren des Vierecks liegt.

Eine ebene, von vier Strecken eingeschlossene Figur heißt Viereck.
Die vier Strecken sind die Seiten des Vierecks. Je zwei benachbarte Seiten haben einen Eckpunkt gemeinsam.

Haben zwei Strecken außer den Endpunkten einen weiteren Punkt gemeinsam, so heißt das Viereck überschlagen.
Ein Viereck heißt konvex, wenn für je zwei Punkte im Inneren des Vierecks auch deren Verbindungsstrecke vollständig im Inneren des Vierecks liegt. Ansonsten nennt man das Viereck nichtkonvex oder konkav.

Überschlagenes, konvexes, konkave Viereck

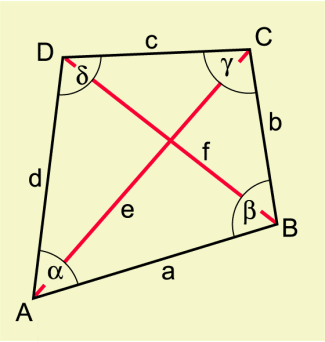
Die Eckpunkte eines (konvexen) Vierecks werden üblicherweise mit Großbuchstaben (z. B. A, B, C und D), die Seiten mit kleinen Buchstaben a, b, c und d sowie die (Innen-)Winkel mit $α, β, γ und δ$ im mathematisch positiven Umlaufsinn bezeichnet, wenn nicht aus dem Kontext andere Bezeichnungen erforderlich sind.
Es sind a und c sowie b und d gegenüberliegende Seiten; a und b, b und c, c und d sowie d und a sind benachbarte Seiten.
Die Verbindungsstrecken nicht benachbarter Eckpunkte (in der Abbildung AC = e und BD = f) sind die Diagonalen des Vierecks.
Es sind $α u n d γ s o w i e β u n d δ$ gegenüberliegende Winkel;
$α u n d β, β u n d γ, γ u n d δ s o w i e δ u n d α$ sind benachbarte Winkel.

Der Umfang u eines Vierecks ABCD ist die Summe der Seitenlängen:
u = a + b + c + d

Allgemeines Viereck

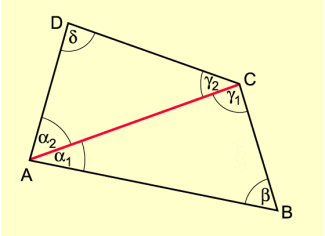
Die Summe der Innenwinkel eines Vierecks ABCD beträgt $360 °$ :
$α + β + γ + δ = 360 °$

Beweis:
Das Viereck ABCD wird durch eine Diagonale in zwei Dreiecke zerlegt, deren Winkelsumme jeweils $180 °$ beträgt:
$Δ A B C : α_{1} + β + γ_{1} = 180 °$
$Δ A C D : α_{2} + γ_{2} + δ = 180 °$
Mit $α_{1} + α_{2} = α u n d γ_{1} + γ_{2} = γ$ gilt dann im Viereck ABCD:
$(α_{1} + α_{2}) + β + (γ_{1} + γ_{2}) + δ = 2 \cdot 180 °$
$α + β + γ + δ = 360 °$ (w. z. b. w. )

Beweisfigur

Stand: 2010
Dieser Text befindet sich in redaktioneller Bearbeitung.

Mathe Note verbessern?

Kostenlos bei Duden Learnattack registrieren und ALLES 48 Stunden testen.

Kein Vertrag. Keine Kosten.

40.000 Lern-Inhalte in Mathe, Deutsch und 7 weiteren Fächern
Hausaufgabenhilfe per WhatsApp
Original Klassenarbeiten mit Lösungen
Deine eigene Lern-Statistik
Kostenfreie Basismitgliedschaft

Mathe kostenlos lernen

Viereck, allgemein

Rechtliches

Einloggen