Zinseszins, Berechnen

Wenn ein Kapital über längere Zeiträume verzinst wird, werden die anfallenden Zinsen im Allgemeinen dem Kapital zugeschlagen und im folgenden Jahr mit verzinst.
Die Rechnung dafür heißt Zinseszinsrechnung.
Dabei wächst ein Anfangskapital $K_0$bei einem Zinssatz p % über einen Zeitraum von n Jahren auf ein Endkapital $K_n$ .
Dafür gilt die folgende Formel:

$K_n=K_0\cdot {\left(\frac{100+p}{100}\right)}^n$

Man setzt

$\frac{100+p}{100}=1+\frac{p}{100}=q$ und nennt q den Zinsfaktor.

Die Formel lautet dann:
$K_n=K_o\cdot q^n$

Wenn man die Ergebnisse nach dieser Formel mit den von Banken gezahlten Zinsen vergleicht, kann man u. U. Differenzen feststellen.
Dies liegt daran, dass im Bankwesen Centbeträge nicht verzinst werden und Zinsen grundsätzlich abgerundet werden.
Wenn man die obige Formel nach q umstellt, erhält man $q=\sqrt[n]{\frac{K_n}{K_0}}$
$1+\frac{p}{100}=q$, kann man dann $p=\left(q-1\right)\cdot 100$ berechnen.

Wenn man die obige Formel nach n umstellt, erhält man:
$n=\frac{\log K_n-\log K_0}{\log q}$

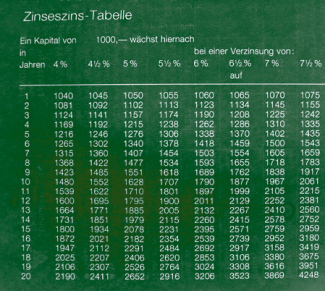
Das schnelle Anwachsen exponentieller Zusammenhänge lässt sich mithilfe des folgenden Beispiels verdeutlichen:
Wenn man zu Beginn unserer Zeitrechnung den Betrag von 1 (man nehme eine beliebige kleine Einheit) zu 3 % angelegt hätte, wäre das Guthaben im Jahr 2000 auf $\mathrm{4,2755}\cdot {10}^{25}$ dieser Einheit angewachsen.
Nimmt man als Einheit 1 Cent, so wäre das ein Betrag von
472 550 000 000 000 000 000 000 Euro. So viel Geld gibt es auf der ganzen Welt nicht.