Zufallsgrößen

Eine Zufallsgröße X ist dadurch charakterisiert, dass sie bei unter gleichen Bedingungen durchgeführten Versuchen verschiedene Werte, von denen jeder ein zufälliges Ereignis ist, annehmen kann. Man unterscheidet zwischen diskreten und stetigen (kontinuierlichen) Zufallsgrößen.

Bei einer diskreten Zufallsgröße sind in einem Intervall nur endlich viele Werte $x_1,x_2\mathrm{...}{x}_n$ möglich. Diese treten jeweils mit der Wahrscheinlichkeit $p_1,p_2\mathrm{...}bzw.p_n$ auf.

Ein Beispiel einer solchen Zufallsgröße ist die Augenzahl A beim Würfeln. Diese kann nur die Werte 1, 2, 3, 4, 5 und 6 annehmen (wobei hier $P\left(X=1\right)=P\left(X=2\right)=\mathrm{...}=P\left(X=6\right)=\frac{1}{6}$ gilt).
Erwartungswert und Varianz, die die entsprechende Wahrscheinlichkeitsverteilung charakterisieren, lassen sich für diskrete Zufallsgrößen mit relativ einfachen mathematischen Mitteln berechnen.

Eine stetige Zufallsgröße dagegen kann in einem Intervall beliebig (unendlich) viele Werte annehmen. Als Beispiel einer stetigen Zufallsgröße lässt sich die Geschwindigkeit von Gasmolekülen anführen, die sich durch Zusammenstoß mit anderen Molekülen stetig ändert.
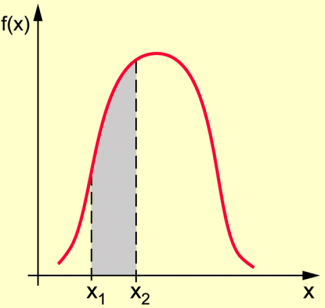
Da die Wahrscheinlichkeit für das Auftreten eines einzelnen Wertes bei stetigen Zufallsgrößen gleich null ist, lassen sich nur Aussagen darüber treffen, mit welcher Wahrscheinlichkeit X zwischen zwei Werten liegt. Dies ist mithilfe der sogenannten Dichtefunktion $f\left(x\right)$ möglich (Bild 1). Diese Funktion schließt mit der x-Achse eine Fläche von 1 ein, und die Wahrscheinlichkeit dafür, dass X zwischen den Werten $x_1$ und $x_2$ liegt, ist dann gleich dem Inhalt der in Bild 1 schraffierten Fläche. Eine Berechnung dieses Wertes ist (nur) mit Mitteln der Integralrechnung möglich. Dies gilt auch für die entsprechende Berechnung von Erwartungswert und Varianz stetiger Zufallsgrößen.