- Lexikon
- Physik Abitur
- 2 Mechanik
- 2.3 Dynamik
- 2.3.2 Die newtonschen Gesetze
- Das newtonsches Grundgesetz (2. newtonsches Gesetz)
Das newtonsches Grundgesetz (2. newtonsches Gesetz)
Dabei ist stets zu beachten:
- Mit der Kraft F ist immer die resultierende Kraft gemeint. Wirken auf einen Körper mehrere Kräfte, dann ist jeweils die Resultierende zu bilden.
- Beschleunigung und beschleunigende Kraft haben immer die gleiche Richtung.
Aus der genannten Gleichung ergibt sich auch die Einheit Newton für die Kraft: Setzt man in die Gleichung die Einheiten für die Masse und die Beschleunigung ein, so erhält man:
Die Einheit Newton (1 N) ist nicht mehr und nicht weniger als eine zweckmäßige Abkürzung für einen längeren Term.
Wirkt auf einen Körper eine resultierende Kraft, so wird er in Richtung dieser Kraft beschleunigt.
Material zum Thema
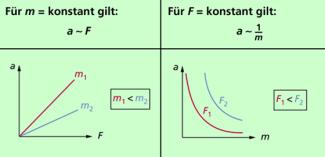
In Alltag und Technik sind insbesondere zwei spezielle Fälle von Interesse, die in Bild 2 dargestellt sind.
Ein Beispiel für die konstante Masse sind Fahrzeuge, bei denen die Beschleunigung jeweils von der wirkenden Antriebskraft abhängig ist. Ein Beispiel für die konstante Kraft ist ein Pkw, der sehr unterschiedlich beladen sein kann und bei dem die Beschleunigung von der Beladung abhängt, konstante Antriebskraft vorausgesetzt.
Die Zusammenhänge zwischen Kraft F, Masse m und Beschleunigung a kann man auch grafisch darstellen.
Die Zusammenhänge zwischen Kraft, Masse und Beschleunigung kann man auch experimentell untersuchen, wobei das mit sehr verschiedenen Experimentieranordnungen möglich ist. Eine Möglichkeit ist in der Simulation dargestellt.
Eine allgemeinere Formulierung des newtonschen Grundgesetzes
Die oben genannte Gleichung ist die, die häufig in den Mittelpunkt gestellt wird. NEWTON selbst hat sein 2. Axiom etwas anders und damit allgemeiner formuliert. Er selbst sprach von der zeitlichen Änderung der Bewegungsgröße. Dahinter steckt folgende Überlegung:
Ersetzt man in der Gleichung die Beschleunigung a durch die zeitliche Änderung der Geschwindigkeit, so erhält man:
Das bedeutet: Die Kraft ist gleich der zeitlichen Änderung des Impulses. Diese Gleichung ist aus folgenden Gründen allgemeiner als die Gleichung : Der Impuls eines Körpers ist definiert als das Produkt aus der Masse eines Körpers und seiner Geschwindigkeit:
Die Änderung des Impulses ist somit:
Diese Impulsänderung beinhaltet sowohl die Möglichkeit der Geschwindigkeitsänderung (Beschleunigung), die auch bei enthalten ist. Sie enthält aber auch die Möglichkeit der zeitlichen Änderung der Masse, während im anderen Fall die Masse als konstant angenommen wird.
Ein Angebot von 