Die Entropie
Reversible und irreversible Vorgänge
In Natur und Technik gehen ständig eine Vielzahl von Vorgänge vor sich, die man in unterschiedlicher Weise einteilen kann. Eine aus physikalischer Sicht ganz wesentliche Unterscheidung ist die zwischen reversiblen und irreversiblen Vorgängen.
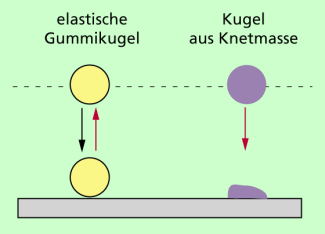
Der Unterschied soll an einem einfachen Gedankenexperiment verdeutlicht werden (Bild1): Zwei Kugeln aus verschiedenem Material fallen aus gleicher Höhe zu Boden. Während die völlig elastische Kugel annähernd wieder ihren Ausgangspunkt erreicht, bleibt die Kugel aus Knetmasse am Boden liegen.
Vorgänge in Natur und Technik, die von einem Ausgangszustand aus von allein wieder zu diesem Ausgangszustand gelangen, bezeichnet man als reversible Vorgänge oder umkehrbare Vorgänge. Solche reversiblen Vorgänge sind z.B. näherungsweise die Bewegung der Erde um die Sonne, ein hin und herschwingendes Fadenpendel während eines kurzen Zeitraumes oder die Bewegung des in Bild dargestellten hochelastischen Balls.
Daneben gibt es aber viele Vorgänge, die von selbst nur in einer bestimmten Richtung ablaufen. Ein Beispiel ist der in Bild 1 dargestellte Körper aus Knetmasse: Es ist nie beobachtet worden, dass ein solcher unelastischer Körper von allein wieder seine ursprüngliche Gestalt annimmt und in seinen Ausgangszustand zurückkehrt, obwohl das mit dem Energieerhaltungssatz vereinbar wäre. Ähnliches gilt für eine Tasse mit heißem Tee: Die Wärmeübertragung erfolgt stets von heißen Tee an die kühlere Umgebung, niemals von selbst in der umgekehrten Richtung. Bei solchen Vorgängen wird der Ausgangszustand von allein nicht wieder erreicht. Vorgänge in Natur und Technik, die von einem Ausgangszustand aus unbeeinflusst in einer bestimmten Richtung ablaufen und bei denen von allein der Ausgangszustand nicht wieder erreicht wird, nennt man irreversible Vorgänge oder auch nicht umkehrbare Vorgänge.
Zusammenfassend kann man einen irreversiblen Vorgang durch folgende Merkmale kennzeichnen:
| (1) | Wärme wird an die Umgebung abgegeben und „zerstreut“ sich dort. |
| (2) | Ein System gelangt in einen Zustand größerer Unordnung. |
| (3) | Die Energie und die Teilchen des Systems nehmen eine wahrscheinlichere Verteilung an. |
Auch bei solchen irreversiblen Vorgängen lässt sich der Ausgangszustand wieder herstellen, allerdings passiert das nicht von allein, sondern durch Eingriffe von außen. Dabei zeigt eine genauere Analyse beliebiger Beispiele: In der Regel verlaufen Vorgänge irreversibel. Reversible Prozesse sind Grenzfälle irreversibler Prozesse.
Betrachtet man reversible und irreversible Vorgänge aus energetischer Sicht, dann gilt:
Der Energieerhaltungssatz erlaubt keine Entscheidung darüber, ob ein Vorgang reversibel oder irreversibel ist. Reversibilität und Irreversibilität von Vorgängen sind nach dem Energieerhaltungssatz möglich. Um irreversible Prozesse genauer kennzeichnen zu können, wurde als neue physikalische Größe die Entropie eingeführt.
Entropie und Wahrscheinlichkeit
Der Begriff Entropie wurde 1865 durch den deutschen Physiker RUDOLF CLAUSIUS (1822-1888) in die Physik eingeführt. CLAUSIUS selbst nutzte für die Größe auch den Terminus „Verwandlungswert“. Sie ist eine Größe, mit deren Hilfe man die Irreversibilität eines Vorganges kennzeichnen kann. Von praktischer Bedeutung ist nicht der absolute Betrag der Entropie S, sondern ihre Änderung. Gemessen wird sie in der Einheit J/K (Joule durch Kelvin).
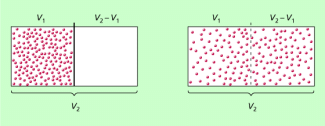
Um das Wesen der Größe Entropie zu klären, wird der in Bild 2 dargestellte Modellversuch betrachtet: In einem Volumen befinden sich Gasteilchen, die von einem gleichgroßen Volumen abgetrennt sind und sich nach Entfernen der Trennwand im gesamten Volumen ausbreiten können. Wartet man eine hinreichend lange Zeit, dann ist zu erwarten, das sich die Gasteilchen im gesamten Volumen gleichmäßig verteilt haben. Eine Gleichverteilung ist die wahrscheinlichste Verteilung. Die Wahrscheinlichkeit dafür, dass sich alle Teilchen wieder im ursprünglichen Volumen versammeln, ist äußerst gering, allerdings nicht null. Diese Zusammenhänge kann man auch quantitativ beschreiben:
Ein zufällig herausgegriffenes Teilchen befindet sich mit einer Wahrscheinlichkeit von
Die Wahrscheinlichkeit, es im halb so großen Volumen
Dasselbe gilt auch für ein beliebiges zweites Teilchen. Die Wahrscheinlichkeit, beide Teilchen gleichzeitig im Volumen zu finden, beträgt dann nur noch:
Allgemein gilt für ein solches sich selbst überlassenes System:
Dieser eben beschriebene Zusammenhang wird für die Definition der Entropie genutzt. Es wird definiert:
Je größer für ein System die Wahrscheinlichkeit ist, desto größer soll die Änderung der Entropie sein, wenn es vom Ausgangszustand in den Endzustand gelangt. Es gilt:
Eine andere Definition der Entropie
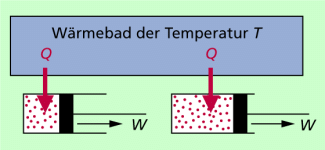
Den oben genannten Zusammenhang kann man für quantitative Betrachtungen von Vorgängen nutzen. Er kann aber schwerlich für eine praktikable Messung der Entropieänderung genutzt werden. Das kann man bei einem anderen Herangehen erreichen. Dazu wird ein Wärmebad der (konstanten) Temperatur T betrachtet, das Wärme an ein Gas abgibt (Bild 3). Der frei bewegliche Kolben verschiebt sich dadurch. Die Gasteilchen verteilen sich in einem größeren Raumbereich. Die Entropie nimmt zu. Es gilt:
Davon ausgehend kann man die Entropieänderung folgendermaßen definieren:
Beispiele für Entropieänderungen
Nachfolgend sind einige elementare Vorgänge genannt und die jeweiligen Entropieänderungen angegeben.
| (1) | Schmelzen und Sieden eines Stoffes: Beim Schmelzen und bei Sieden eines Stoffes wird bei einer bestimmten Temperatur (Schmelztemperatur, Siedetemperatur) Wärme zugeführt. Die Unordnung der Teilchen wird größer. Die Entropie vergrößert sich. |
| (2) | Temperaturausgleich zwischen zwei Körpern: Es wird insgesamt ein wahrscheinlicherer Zustand angenommen. Die Entropie vergrößert sich. |
| (3) | Kondensieren und Erstarren eines Stoffes: Beim Kondensieren und Erstarren wird bei einer bestimmten Temperatur Wärme an die Umgebung abgegeben. Die Ordnung der Teilchen wird größer. Die Entropie nimmt ab. |
Der Wärmetod - Was ist das?
Nachdem Ende des 19. Jahrhunderts die physikalische Bedeutung der Entropie erkannt wurde, verbreitete sich auch in der physikalischen Literatur eine Vorstellung, die die Menschen in Angst und Schrecken versetzte: Wenn das Universum ein abgeschlossenes System ist, dann nimmt in ihm die Entropie beständig zu. Irgendwann müsste das Universum dann einen Zustand erreichen, bei dem ein vollständiger Temperaturausgleich zwischen allen Körpern eingetreten ist. Das gesamte Universum wäre dann ein Wärmebad mit konstanter und sehr niedriger Temperatur. Es könnten keine weiteren Änderungen erfolgen. In der Welt würde sich nichts mehr bewegen. Insbesondere wäre auch kein Leben mehr möglich. Dieser Zustand wurde als Wärmetod bezeichnet.
Ob unserem Universum ein Wärmetod bevorsteht und wann er eintreten könnte, sind Fragen, die selbst heute nicht eindeutig beantwortet werden können. Wir wissen aber: Die Sonne wird der Erde noch mehrere Milliarden Jahre Wärme und Licht spenden und damit alle Prozesse auf der Erde aufrechterhalten. Allerdings könnte das Universum in einer sehr fernen Zukunft tatsächlich einen Wärmetod erleiden. Gegenwärtig weiß man aber noch gar nicht, ob das Universum tatsächlich ein abgeschlossenes physikalisches System ist. Deshalb ist es durchaus möglich, dass ihm eine andere Zukunft als der Wärmetod bevorsteht. Es könnte sogar recht heiß enden.
Ein Ausblick: Der Mensch als thermodynamisches System
Physikalisch betrachtet ist der Mensch ein komplexes, hoch organisiertes, offenes System. Er nimmt Stoff (Nahrung), damit auch Energie und Entropie auf und exportiert diese auch wieder (Bild 5).
Stoffe werden in Form von Nahrung und Getränken aufgenommen, durch Ausscheidungen werden Stoffe abgegeben. Konstantes Gewicht vorausgesetzt, ist die Summe der aufgenommenen Stoffe gleich der Summe der ausgeschiedenen Stoffe.
Mit der Nahrung erfolgt eine Energieaufnahme. Für den Grundumsatz, d.h. zur Aufrechterhaltung der Lebensfunktionen, ist im Durchschnitt eine Energie von 6.500 kJ pro Tag erforderlich. Die gleiche Energie wird auch wieder abgegeben, meist in Form von Wärme an die Umgebung (Wärmestrahlung, Wärmeleitung). Die mit der Nahrung aufgenommene Energie ist in der Regel hochwertige Energie, die in den organischen Substanzen der Lebensmittel gespeichert ist. Diese Energie wird durch den Verdauungsprozess entwertet. Damit ist eine Entropieerhöhung verbunden. Mit der Abgabe der entwerteten Energie an die Umgebung wird auch Entropie exportiert.
Der Entropieexport eines Menschen ist beträchtlich. Er kann mit folgender Gleichung berechnet werden:
Das ist der auf den Grundumsatz bezogene Entropieexport. Dieser Entropieexport ist Voraussetzung dafür, dass sich ein Mensch entwickeln kann.
Berechnung Energieimport Wärmetod Energieerhaltungssatz Temperaturausgleich thermodynamische Wahrscheinlichkeit Energieexport Kondensieren Reversibilität irrreversible Vorgänge umkehrbare Vorgänge Erstarren Entropie Mensch als thermodynamisches System nicht umkehrbare Vorgänge Sieden reversible Vorgänge Entropieexport Irreversibilität RUDOLF CLAUSIUS Rechenbeispiel Verwandlungswert Schmelzen Entropieimport
Ein Angebot von 