Energie und Arbeit im Gravitationsfeld

Um eine Weltraumstation oder einen Satelliten in den Orbit zu bringen, ist eine bestimmte Arbeit im Gravitationsfeld der Erde erforderlich. Darüber hinaus muss der Station oder dem Satelliten eine bestimmte Geschwindigkeit verliehen werden, damit sie sich auf einer stabilen Bahn bewegen. Die Körper besitzen damit potenzielle und kinetische Energie. Arbeit und potenzielle Energie im Gravitationsfeld können mithilfe des Gravitationsgesetzes berechnet werden, die kinetische Energie ergibt sich aus der Masse und der Geschwindigkeit des Körpers.

Gravitationsgesetz

#Gravitation #Ortsfaktor #Planet #Mond #Sonne #Satellit #Gravitationsgesetz

Wir betrachten nachfolgend die Arbeit im Gravitationsfeld der Erde. Für andere Himmelskörper gelten die gleichen Überlegungen. Darüber hinaus ist es für die Erde sinnvoll, zwischen dem oberflächennahen Bereich und größeren Raumbereichen zu differenzieren.

Arbeit und potenzielle Energie in der Nähe des Erdbodens

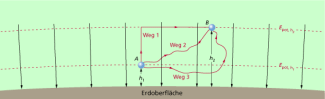
Unter „Nähe des Erdbodens“ verstehen wir den normalen Lebensbereich des Menschen, also den Bereich bis etwa 10 km Höhe über NN. In diesem Bereich kann man das Gravitationsfeld der Erde näherungsweise als ein homogenes Feld ansehen (Bild 2). Damit kann in diesem Bereich der Ortsfaktor (Fallbeschleunigung, Erdbeschleunigung) als konstant angesehen werden. Gleich ist damit auch die Gewichtskraft eines Körpers. Soll ein Körper aus der Höhe $h_{1}$ in die Höhe $h_{2}$ gehoben werden, ist dazu Hubarbeit erforderlich:

$\begin{array}{l} W = F_{G} \cdot Δ h = m \cdot g \cdot Δ h \\ F_{G} Gewichtskraft des Körpers \\ Δ h Höhenunterschied \\ m Masse des Körpers \\ g Ortsfaktor (Fallbeschleunigung) \end{array}$

Aus dem allgemeinen Zusammenhang zwischen Arbeit und Energie ergibt sich, dass die verrichtete Arbeit gleich der Änderung der potenziellen Energie ist. Demzufolge kann man schreiben:

$W = Δ E_{p o t} = F_{G} \cdot Δ h = m \cdot g \cdot Δ h$

Dabei ist zu beachten:

Die verrichtete Arbeit und damit die Änderung der potenziellen Energie ist nur vom Anfangspunkt und vom Endpunkt der Bewegung, also vom Höhenunterschied, abhängig (Bild 2). Beide Größe hängen nicht von der Bahn ab, auf der der Körper von A nach B verschoben wird.

Auf den gestrichelt eingezeichneten Äquipotenziallinien (Bild 2) ist die potenzielle Energie jeweils gleich. Bei einer reibungsfreien Verschiebung eines Körpers längs einer Äquipotenziallinie wird keine Arbeit verrichtet.

Wird ein Körper gehoben, so muss am Körper Arbeit verrichtet werden. Erfolgt die Bewegung in Richtung Erde, so ist der Körper in der Lage, Arbeit zu verrichten.

Die Änderung der potenziellen Energie besagt nichts darüber, welchen (absoluten) Wert diese Energie in einem bestimmten Punkt hat. Dieser Wert ist davon abhängig, welches Bezugsniveau man für die potenzielle Energie wählt. Häufig nimmt man die Erdoberfläche als Bezugsniveau und setzt dafür die potenzielle Energie gleich null. Es kann aber auch jedes andere Bezugsniveau angenommen werden, z.B. ein Punkt im Unendlichen.

Arbeit und potenzielle Energie in einem größeren Raumbereich

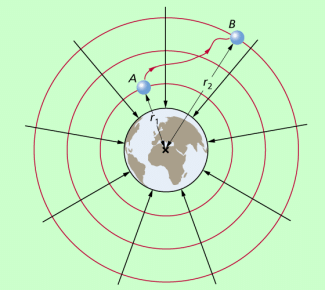
Bei einem größeren Raumbereich ist zu beachten, dass das Gravitationsfeld der Erde wie das eines jeden kugelförmigen Himmelskörpers ein Radialfeld ist. Der Ortsfaktor (Fallbeschleunigung) ist nicht konstant. Demzufolge ist auch die Gravitationskraft auf einen Körper bestimmter Masse unterschiedlich. Wenn man die Arbeit zum Verschieben eines Körpers von A nach b berechnen will, muss man demzufolge von der allgemeinen Definition der mechanischen Arbeit ausgehen:
$\begin{array}{l} W = \int_{s_{1}}^{s_{2}} F d s \\ Statt des Weges s wählen wir den Abstand r \\ vom Erdmittelpunkt . Für die Kraft F gilt das \\ Gravitationsgesetz F = G \frac{m \cdot M}{r^{2}} . \\ Damit erhält man: \\ W = \int_{r_{1}}^{r_{2}} G \frac{m \cdot M}{r^{2}} d r oder \\ W = G \cdot m \cdot M \int_{r_{1}}^{r_{2}} \frac{1}{r^{2}} d r \\ Die Integration ergibt: \\ W = G \cdot m \cdot M \cdot {[- \frac{1}{r}]}_{r_{1}}^{r_{2}} \\ W = G \cdot m \cdot M \cdot (\frac{1}{r_{1}} - \frac{1}{r_{2}}) \end{array}$
Nach dem allgemeinen Zusammenhang zwischen Arbeit und Energie ist die Änderung der potenziellen Energie gleich der verrichteten Arbeit. Deshalb kann man allgemein formulieren:

In einem radialen Gravitationsfeld kann die Arbeit zum Verschieben eines Körpers und damit die Änderung seiner potenziellen Energie berechnet werden mit der Gleichung:
$\begin{array}{l} W = Δ E_{p o t} = G \cdot m \cdot M \cdot (\frac{1}{r_{1}} - \frac{1}{r_{2}}) \\ G Gravitationskonstante \\ m Masse des Körpers, der bewegt wird \\ M Masse des felderzeugenden Körpers \\ r_{1}, r_{2} Entfernung vom Massenmittelpunkt des \\ felderzeugenden Körpers \end{array}$
Auch in diesem Falle ist die verrichtete Arbeit und damit die Änderung der potenziellen Energie nur vom Anfangspunkt und vom Endpunkt abhängig und wird nicht durch die Bahn beeinflusst, auf der der Körper bewegt wird.

Beispiel: Satellit, der in eine Erdumlaufbahn gebracht wird
Betrachten wir als Beispiel einen Satelliten mit einer Masse von 1000 kg, der von der Erdoberfläche aus in eine kreisförmige Erdumlaufbahn in 300 km Höhe über der Erdoberfläche gebracht werden soll.

Verrichtete Arbeit im Gravitationsfeld: Die Arbeit im Gravitationsfeld kann nach der obigen Gleichung berechnet werden, wobei m die Masse des Satelliten und M die Masse der Erde ist.
$\begin{array}{l} W = G \cdot m \cdot M \cdot (\frac{1}{r_{1}} - \frac{1}{r_{2}}) \\ W = \frac{6,673 m^{3}}{10^{11} kg \cdot s^{2}} \cdot 1000 kg \cdot 5,97 \cdot 10^{24} kg \cdot (\frac{1}{6,371 \cdot 10^{6} m} - \frac{1}{6,671 \cdot 10^{6} m}) \\ W = \frac{6,673 m^{3}}{10^{11} kg \cdot s^{2}} \cdot 1000 kg \cdot 5,97 \cdot 10^{24} kg \cdot \frac{7,06}{10^{9} m} \\ W = 2,81 \cdot 10^{9} \frac{kg \cdot m^{2}}{s^{2}} = 2,81 \cdot 10^{9} J \end{array}$
Um diesen Wert vergrößert sich auch die potenzielle Energie, wenn man diese an der Erdoberfläche null setzt.

Verhältnis von potenzieller und kinetischer Energie zueinander: Ein umlaufender Satellit besitzt nicht nur potenzielle Energie, sondern aufgrund seiner Bewegung um die Erde auch kinetische Energie. In welchem Verhältnis stehen bei einem Satelliten potenzielle und kinetische Energie zueinander? Wir gehen dabei von dem gleichen Satelliten aus. Seine potenzielle Energie wurde oben berechnet. Die kinetische Energie ergibt sich aus Masse und Geschwindigkeit. Die Geschwindigkeit lässt sich ermitteln, indem man die Radialkraft gleich der Gravitationskraft setzt:
$\begin{array}{l} \frac{m \cdot v^{2}}{r} = \frac{G \cdot m \cdot M}{r^{2}} \\ Die Umstellung nach v ergibt: \\ v = \sqrt{\frac{G \cdot M}{r}} \\ v = \sqrt{\frac{6,673 m^{3} \cdot 5,97 \cdot 10^{24} kg}{10^{11} kg \cdot s^{2} \cdot 6,671 \cdot 10^{6} m}} \\ v = 7,73 \cdot 10^{3} \frac{m}{s} \end{array}$
Damit erhält man für die kinetische Energie:
$\begin{array}{l} E_{k i n} = \frac{m \cdot v^{2}}{2} \\ E_{k i n} = \frac{1000 kg \cdot {(7,73 \cdot 10^{3} m)}^{2}}{2} \\ E_{k i n} = 29,8 \cdot 10^{9} J \end{array}$
Der Vergleich zeigt: Die kinetische Energie des Satelliten ist etwa 10-mal so groß wie seine potenzielle Energie.

Physik Note verbessern?

Kostenlos bei Duden Learnattack registrieren und ALLES 48 Stunden testen.

Kein Vertrag. Keine Kosten.

40.000 Lern-Inhalte in Mathe, Deutsch und 7 weiteren Fächern
Hausaufgabenhilfe per WhatsApp
Original Klassenarbeiten mit Lösungen
Deine eigene Lern-Statistik
Kostenfreie Basismitgliedschaft

Physik kostenlos lernen

Verwandte Artikel

Angaben zum Lexikon

Impressum

Energie und Arbeit im Gravitationsfeld

Gravitationsgesetz

Arbeit und potenzielle Energie in der Nähe des Erdbodens

Arbeit und potenzielle Energie in einem größeren Raumbereich

Rechtliches

Einloggen