Hydraulische Anlagen
Hydraulische Anlagen
Hydraulische Anlagen sind kraftumformende Einrichtungen, bei denen die gleichmäßige und allseitige Ausbreitung des Druckes in Flüssigkeiten genutzt wird. Dabei werden durch Kolbendruck Kräfte übertragen sowie deren Betrag oder deren Richtung oder beides geändert.
Pkw auf einer hydraulischen Hebebühne
Hydraulische Anlagen - Mechatronische Arbeiten
L. Meyer, Potsdam
Aufbau und Wirkungsweise
Eine hydraulische Anlage besteht aus zwei unterschiedlich großen Zylindern mit beweglichen Kolben, die durch eine Leitung miteinander verbunden sind (Bild 2). In den Zylindern und in der Leitung befindet sich Öl oder eine andere Flüssigkeit. Man nennt solche für hydraulische Anlagen genutzte Flüssigkeit auch Hydraulikflüssigkeit.
Erzeugt man an einem Kolben einen Kolbendruck, so tritt dieser Druck in der gesamten Flüssigkeit und auch am anderen Kolben auf, denn in einer abgeschlossenen Flüssigkeit ist der Druck überall gleich groß und breitet sich allseitig aus. Damit gilt für den Druck an den beiden Kolben:
Setzt man in diese Gleichung für den Druck den Quotienten aus jeweiliger Kraft F und Fläche A ein, so erhält man das Gesetz für hydraulische Anlagen. Es besagt:
Aufbau einer hydraulischen Anlage
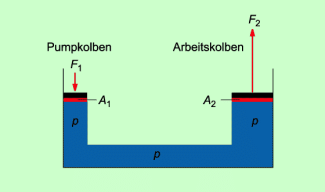
Für jede hydraulische Anlage im Gleichgewicht gilt:
Die an den Kolben wirkenden Kräfte verhalten sich wie die Flächen der Kolben, mit anderen Worten: Auf einen Kolben mit größerer Fläche wirkt eine größere Kraft als auf einen Kolben mit kleinerer Fläche. Man kann auch sagen: Mit einer kleinen Kraft am Kolben mit der kleinen Fläche (Pumpkolben) kann man eine große Kraft am Kolben mit der großen Fläche (Arbeitskolben) hervorrufen.
Wie bei allen kraftumformenden Einrichtungen gilt auch für hydraulische Anlagen die Goldene Regel der Mechanik:
Was man an Kraft spart, muss man an Weg zusetzen.
Bei Vernachlässigung der Reibung ist die Arbeit am Pumpkolben genauso groß wie die Arbeit am Arbeitskolben.
Material zum Thema
Beispiel: Hydraulische Presse
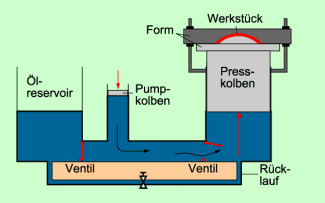
Eine hydraulische Presse dient dazu, um z. B. Bleche in eine bestimmte Form zu bringen. Auf diese Weise stellt man Karosserieteile für PKW her. Der Aufbau einer solchen Presse ist in vereinfachter Form in Bild 3 dargestellt.
Mit dem Pumpkolben wird in der Flüssigkeit ein Druck hervorgerufen, der auch auf den Arbeitskolben (Presskolben) wirkt. Da die Fläche des Presskolbens wesentlich größer ist als die Fläche des Pumpkolbens, ist nach dem Gesetz für hydraulische Anlagen auch die Kraft am Presskolben wesentlich größer als die am Pumpkolben. Das Werkstück, z. B. ein Blech, wird mit großer Kraft in eine Form gedrückt und nimmt damit diese Form „auf kaltem Wege“ an.
Aufbau einer hydraulischen Presse
Weitere Anwendungen
Weitere Beispiele für hydraulische Anlagen sind hydraulische Hebebühnen, hydraulische Wagenheber oder hydraulische Bremsen. Bei Baggern und LKW werden ebenfalls hydraulische Anlagen genutzt, z. B. zum Heben des Baggerarmes, zur Betätigung des Greifers oder zum Abheben der Ladefläche eines LKW.
Auch die Bremsen von PKW und LKW sind hydraulische Anlagen. Genauere Informationen zu Bremsen sind unter diesem Stichwort zu finden.
Pneumatische Anlagen
Anlagen, die nicht mit einer Flüssigkeit, sondern mit Druckluft arbeiten, bezeichnet man als pneumatische Anlagen. Solche pneumatischen Anlagen nutzt man z. B. für die Betätigung von Bremsen bei Zügen oder für die Betätigung des Schließmechanismus von Bustüren. Sie sind ähnlich aufgebaut wie hydraulische Anlagen. Es gelten auch die oben genannten Gesetze und Zusammenhänge.
kraftumformende Einrichtung Zylinder Berechnung Kolbendruck Gesetz für hydraulische Anlagen Arbeitskolben pneumatische Anlagen hydraulische Bremse hydraulische Anlagen hydraulische Presse Rechenbeispiel Kolben Hydraulikflüssigkeit Goldene Regel der Mechanik Pumpkolben
Stand: 2010
Dieser Text befindet sich in redaktioneller Bearbeitung.
Ein Angebot von 