Kondensatoren
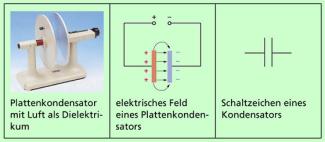
Grundsätzlich besteht ein Kondensator aus zwei Metallplatten, zwischen denen sich ein Isolator, das Dielektrikum, befindet. Die einfachste Form eines Kondensators ist ein Plattenkondensator, der aus zwei sich gegenüberstehenden, voneinander isolierten Metallplatten besteht, zwischen denen Luft ist. Wird zwischen diesen Metallplatten eine elektrische Spannung angelegt, dann sammeln sich auf ihren Oberflächen getrennt voneinander positive und negative Ladungen an. Zwischen den Platten baut sich ein elektrisches Feld auf, in dem Feldenergie gespeichert ist (Bild 1).
Achtung: In einem Kondensator können teilweise beträchtliche Ladungsmengen gespeichert sein. Diese Ladungen können auch noch vorhanden sein, wenn der Kondensator längere Zeit nicht mit einer elektrischen Quelle verbunden war. Berührt man die Anschlüsse eines solchen Kondensators, können kurzzeitig hohe Entladungsströme fließen. Außerdem erreicht die Spannung zwischen den Kondensatorplatten mitunter beträchtliche Werte. Deshalb gilt:
Berühren Sie niemals die Anschlüsse eines Kondensators, wenn Sie nicht sicher sind, ob er sich noch im aufgeladenen Zustand befindet!
Bauformen von Kondensatoren
Neben Plattenkondensatoren, der aus zwei gleich großen, sich parallel gegenüberstehenden Platten bestehen, gibt es eine Reihe weiterer Bauformen, die in der Übersicht in Bild 2 dargestellt sind.
Blockkondensatoren: Um Kondensatoren mit möglichst kleinen Abmessungen zu bauen, ersetzt man die stabilen Metallplatten durch dünne und biegsame Metallfolien. Zwischen sie wird eine isolierende Schicht aus Papier oder Kunststoff gelegt und die drei Folien anschließend zusammengerollt. Deshalb nennt man solche Kondensatoren häufig auch Wickelkondensatoren . Sie haben trotz ihrer kompakten Bauweise recht hohe Kapazitäten, denn die genutzte Fläche ist relativ groß, der Abstand zwischen den Platten hingegen sehr klein.
Keramikkondensatoren: Zur Herstellung von Keramikkondensatoren dampft man auf eine keramische Isolierschicht zwei leitende Schichten auf. Keramikkondensatoren finden in vielen elektronischen Baugruppen Anwendung.
Drehkondensatoren: Für viele technische Anwendungen benötigt man Kondensatoren, deren Kapazität regulierbar ist. Das bekannteste Beispiel ist der elektrische Schwingkreis im Empfangsteil eines Radios, den man auf die Frequenz des Senders abstimmt, indem die Kapazität des Kondensators verändert wird. Drehkondensatoren bestehen aus einem festen und einem drehbar gelagerten Plattensatz. Mithilfe einer Regulierungsschraube kann man den beweglichen Plattensatz zwischen die unbeweglichen Platten schieben. Die Kapazität des Drehkondensators erhöht sich dabei, denn Ladungs- und Feldspeicherung erfolgen im Wesentlichen nur in demjenigen Teil des Kondensators, in dem sich die Platten direkt gegenüberstehen.
Daneben gibt es weitere spezielle Arten. Ein Kugelkondensator besteht aus zwei konzentrisch angeordneten Kugeln. Er findet vor allem in Großbauweise zur Speicherung größerer Ladungsmengen Anwendung. Historisch bedeutsam ist eine Leidener Flasche . Darunter versteht man einen zylinderförmigen (flaschenförmigen) Kondensator. Der Glaszylinder ist innen und außen mit Stanniolpapier beklebt, das Glas bildet das Dielektrikum.
Solche Leidener Flaschen haben eine hohe Durchschlagfestigkeit und werden noch heute bei Influenzmaschinen verwendet. Für größere Kapazitäten verwendet man Elektrolytkondensatoren.
Die Kapazität von Kondensatoren
Die Kapazität C oder das Speicherungsvermögen eines Kondensators hängt allgemein davon ab, wie viel Ladung Q bei einer bestimmten Spannung gespeichert wird. Es gilt:
Bei einem Plattenkondensator hängt die Kapazität davon ab, wie groß die Platten sind, welchen Abstand sie voneinander haben und welcher Stoff sich zwischen ihnen befindet. Für die Kapazität eines solches Plattenkondensators gilt:
Aufladen und Entladen von Kondensatoren
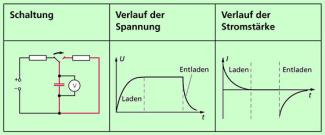
Wird ein Kondensator an eine Gleichspannungsquelle angeschlossen, dann lädt er sich auf. Es fließt ein Ladestrom, zwischen den Platten des Kondensators liegt eine Spannung an. Der zeitliche Verlauf von Spannung und Stromstärke ist in Bild 3 dargestellt. Die Ladekurven und die Entladekurven lassen sich auch mathematisch beschreiben.
Für das Aufladen eines Kondensators (Bild 3) gilt:
In analoger Weise gilt für das Entladen eines Kondensators (Bild 3):
Schaltung von Kondensatoren
Mehrere Kondensatoren können parallel oder in Reihe geschaltet werden. Die betreffenden Gesetze ähneln denen für Widerstände bei Parallel- oder Reihenschaltung. Sie sind in der nachfolgenden Übersicht zusammengestellt.
Energie des elektrischen Feldes eines Kondensators und elektrische Feldstärke in ihm
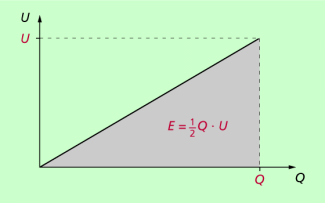
Die in einem Kondensator gespeicherte Feldenergie hängt von der gespeicherten Ladung und der Spannung ab. Allgemein gilt für die elektrische Energie:
Das ist die Energie, die zum Aufladen eines Kondensators erforderlich ist. Es ist damit zugleich die in ihm gespeicherte Feldenergie. Die Gleichung kann man aus der grafischen Darstellung (Bild 4) ableiten. Es gilt:
Die elektrische Feldstärke in einem Kondensator hängt von seinem Aufbau ab. In einem Platenkondensator ist das elektrische Feld homogen. Für einen solchen Kondensator gilt für die elektrische Feldstärke:
Achtung: Sowohl die Energie als auch die elektrische Feldstärke haben das Kurzzeichen E. In der Regel geht es dem Zusammenhang oder aus der Einheit hervor, welche Größe gemeint ist. Die Feldstärke hat die Einheit V/m, die Energie die Einheit J.
Kondensator im Gleich- und Wechselstromkreis
Legt man an einen Kondensator im Gleichstromkreis eine Spannung an, so lädt er sich auf. Verbindet man die Anschlüsse miteinander, so entlädt er sich.
Durch den Kondensator hindurch fließt aber kein Strom. Er bildet im Gleichstromkreis einen unendlich großen Widerstand.
Im Wechselstromkreis dagegen kommt es zu einem ständigen Auf- und Entladen. Im Gesamtstromkreis wirkt das so, als ob sich ein zusätzlicher (endlicher) Widerstand im Stromkreis befindet. Genauere Informationen dazu sind in dem Beitrag „Kapazitive Widerstände“ zu finden.
Berechnung elektrische Feldstärke in einem Kondensator Blockkondenstoren Speicherungsvermögen eines Kondensators Plattenkondensatoren Kapazität eines Kondensators Entladen eines Kondensators Ladestrom Leidener Flaschen Energie eines Kondensators Energie des elektrischen Feldes Kondensatoren Entladestrom Kondensator im Gleichstromkreis Influenzmaschinen Keramikkondensatoren elektrisches Bauelement Kugelkondensatoren Aufladen eines Kondensators Elektrolytkondensatoren Wickelkondensatoren Kondensator im Wechselstromkreis Rechenbeispiel Schaltung von Kondensatoren Feldenergie
Ein Angebot von 