- Lexikon
- Physik Abitur
- 2 Mechanik
- 2.6 Impuls und Drehimpuls
- 2.6.1 Kraftstoß, Impuls und Impulserhaltungssatz
- Raketenantrieb und Raketengrundgleichung
Raketenantrieb und Raketengrundgleichung
Zum Antrieb von Raketen wird das Rückstoßprinzip, auch Raketenprinzip genannt, genutzt. Die physikalische Grundlage ist der Impulserhaltungssatz.
Impulserhaltung und Rückstoß
Feuert man aus einem Gewehr eine Kugel ab, dann spürt man deren Rückstoß. Für das System Gewehr-Kugel gilt der Impulserhaltungssatz: Der Gesamtimpuls ist null oder in anderer Formulierung: Der Impuls ist vor dem Abschuss genauso groß wie nach dem Abschuss.
Allgemein gilt für ein abgeschlossenes System aus zwei Körpern, zwischen denen nur innere Kräfte wirken, dass die Summe ihrer Impulse vor und nach der Wechselwirkung konstant ist. War der Gesamtimpuls der beiden Körper zunächst null, dann muss er auch dann null bleiben, wenn sich beide Körper in entgegengesetzten Richtungen voneinander entfernen.
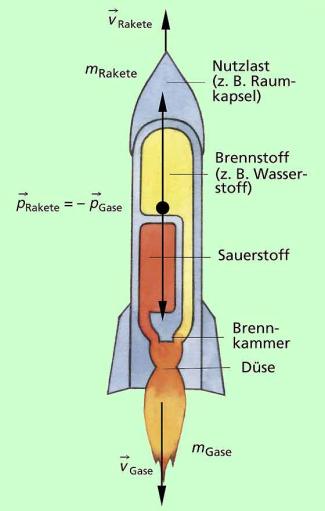
Das gilt auch für eine Rakete: Das abgeschlossene System besteht aus dem Raketenkörper und dem Treibstoff. Der Gesamtimpuls des Systems ist zunächst null. Daran ändert sich auch nichts, wenn die Triebwerke gezündet werden und Verbrennungsgase durch die Düsen mit hoher Geschwindigkeit ausströmen.
Dann gilt für die Impulse (Bild 2):
Bei einer Rakete verändert sich aber aufgrund der ausströmenden Verbrennungsgase ständig die Masse. Deshalb kann der Impulserhaltungssatz in der genannten einfachen Form nur für kurze Zeitintervalle angewendet werden. Das gilt natürlich dann auch für die Gleichung zur Berechnung der Raketengeschwindigkeit.
Die Raketengrundgleichung
Beachtet man die Masseänderung bei der Rakete, dann gilt:
In der zuerst genannten Gleichung bedeuten dM die relativ geringfügige Gasmasse, die während einer sehr kurzen Zeitspanne ausströmt, und dv die kleine Änderung der Geschwindigkeit, die die Rakete in dieser sehr kurzen Zeitspanne erfährt. Die genannte Gleichung ist eine Differenzialgleichung, die durch Integrieren gelöst werden kann. Als Resultat erhält man für die Endgeschwindigkeit der Rakete eine Gleichung, die als Raketengrundgleichung bezeichnet wird. Sie lautet:
Liegt bereits eine Anfangsgeschwindigkeit vor, so kommt diese zur Geschwindigkeit der Rakete hinzu. Die Endgeschwindigkeit kann erhöht werden, wenn man die Ausströmgeschwindigkeit der Gase steigert und das Verhältnis von Startmasse zur Endmasse möglichst groß wählt. Dies bedeutet nichts anders, als möglichst viel Treibstoff und möglichst wenig Nutzlast mitzuführen - ein Grundproblem der Raumfahrt, die natürlich das entgegengesetzte Ziel bei hohen Endgeschwindigkeiten anstrebt.
Die Verbrennungsgase strömen mit hoher Geschwindigkeit in der einen Richtung, die Rakete bewegt sich in der entgegengesetzten Richtung.
Raketenantrieb und Raketengrundgleichung - Grafik
Jens Prockat, Berlin
Historisches zur Raketengrundgleichung
Die Raketengrundgleichung geht auf den britischen Mathematiker WILLIAM MOORE zurück, der sie 1810 veröffentlichte. Davon unabhängig veröffentlichte sie der russische Raumfahrtpionier KONSTANTIN ZIOLKOWSKI im Jahr 1903. Ihm war schon im Jahre 1883 aufgefallen, dass die Raumfahrt nur durch die Anwendung des Impulserhaltungssatzes möglich sein würde. Er führte dazu zahlreiche Experimente in einem kleinen Privatlabor durch und unterbreitete Vorschläge zur Durchführung von Raumfahrtunternehmungen. Beispielsweise erwähnte er als Erster die Möglichkeit des Einsatzes von künstlichen Erdsatelliten. Die Raketengleichung wurde dazu auch von dem deutschen Raketentechniker HERMANN OBERTH und von dem amerikanischen Raketentechniker ROBERT GODDARD unabhängig voneinander hergeleitet.
Arten von Triebwerken bei Raketen
Bei Raketen und in der Raumfahrtechnik insgesamt nutzt man unterschiedliche Triebwerke. Nachfolgend ist dazu ein Überblick gegeben.
Verbrennungstriebwerke: Die weitaus meisten Raketenmotoren nutzen die chemische Energie ihrer Treibstoffe. Dazu werden der Brennstoff und der Oxidator, der den für die Verbrennung nötigen Sauerstoff liefert, zusammengebracht und verbrannt. In einem Feststofftriebwerk, der ältesten Form der Antriebe, liegen Brennstoff und Oxidator als feste oder pastenähnliche Masse vor. Ein solches Triebwerk hat einen einfachen Aufbau, ist betriebssicher und preiswert. Nachteil ist, dass es - einmal gezündet - nicht mehr gestoppt und der Schub kaum dosiert werden kann. Es wird meist als Starthilferakete (»Booster«) für große Trägerraketen eingesetzt.
Das Flüssigkeitstriebwerk ist dagegen wesentlich aufwändiger: Die Treibstoffe (Oxidator und Brennstoff) werden in getrennten Tanks aufbewahrt, durch ein Leitungssystem in die Brennkammer eingespritzt und dort verbrannt. Brennkammer und Ausströmdüse müssen gekühlt werden. Da sie sich relativ einfach regulieren lassen und ihre Ausströmgeschwindigkeit wesentlich höher ist als bei Feststofftriebwerken, werden sie hauptsächlich in den Oberstufen von Trägerraketen und als Steuertriebwerke eingesetzt.
Eine Mischform ist das Hybridtriebwerk, bei dem eine Treibstoffkomponente (meist der Brennstoff) fest vorliegt, während die andere Komponente in flüssiger Form eingespritzt wird.
Die Triebwerke von Trägersystemen können dabei in sehr unterschiedlicher Weise kombiniert und angeordnet werden.
Pressgastriebwerke: Eine relativ einfache und heute ebenfalls genutzte Antriebsquelle stellen Presslufttanks dar, deren Inhalt durch eine Düse ausströmt. Der große Vorteil dieser Methode besteht darin, dass sie sehr unanfällig ist. Insbesondere das Einfrieren des Treibgases stellt kein Problem dar, sofern man einen geeigneten Stoff verwendet. Daher werden solche Triebwerke in Satelliten eingesetzt. Die manövrierfähigen Raumanzüge für Weltraumausstiege amerikanischer Astronauten verfügen ebenfalls über diese Technologie.
Alternative Antriebsquellen: Neben der Verbrennung von chemischen Treibstoffen sind noch zahlreiche Varianten des Raketentriebwerks möglich. Ein thermonukleares Triebwerk wird so betrieben, dass mit der von einem Kernreaktor freigesetzten Wärme ein Arbeitsgas (Wasserstoff oder Helium) erhitzt und zur Düse geleitet wird. Dort sinkt der Druck schlagartig (das Gas wird „entspannt“) und das Gas strömt mit hoher Geschwindigkeit aus. Solche Aggregate wurden in den sechziger Jahren zwar als Experimentalmodell am Boden getestet, allerdings aus Sicherheits-, Kosten- und Umweltgründen nicht zu einsatztauglichen Systemen weiterentwickelt.
Dampftriebwerke hat man allerdings für Höhenraketen seit dieser Zeit noch weiter getestet. Als Wärmequelle dient aber nicht eine thermonukleare Reaktion.
Elektrische Antriebsquellen: Sie werden für Lageregelungen und Bahnkorrektur von Satelliten verwendet. Der elektrostatische Antrieb (Ionentriebwerk) verwendet ein Arbeitsmedium (zum Beispiel Caesium oder Quecksilber), dessen Moleküle durch Hitze ionisiert und dann durch ein elektrisches Feld beschleunigt werden. Nach demselben Prinzip arbeiten Plasmatriebwerke; hier wird zuerst ein Plasma (ein elektrisch geladenes Gas) erzeugt, das dann von elektromagnetischen Feldern hoch beschleunigt und ausgestoßen wird. Beim Lichtbogentriebwerk wird ein Arbeitsmedium mithilfe eines elektrischen Lichtbogens stark erhitzt und an der Düse entspannt.
Als „Sonnensegler“ bezeichnet man Raumfahrzeuge, die durch den Lichtdruck des Sonnenlichts angetrieben werden. Allen diesen Antrieben ist gemeinsam, dass sie nur geringe Schubkraft entwickeln und nicht für den Start vom Erdboden geeignet sind. Im All jedoch können sie ein Raumfahrzeug bei sehr langen Beschleunigungszeiten auf nennenswerte Geschwindigkeiten bringen.
Brennstoff Flüssigkeitstriebwerk KONSTANTIN EDUAROWITSCH ZIOLKOWSKI Raketenantrieb Booster Raumfahrt Pressgastriebwerk Feststoffrakete Raketengrundgleichung Ionentriebwerk Sonnensegler abgeschlossenes System Raketenmotoren Feststofftriebwerk Nutzlast Oxidator Plasmatriebwerk Endgeschwindigkeit Lichtdruck Differenzialgleichung Hybridtriebwerk Raumfahrzeuge Treibstoff Flüssigkeitsrakete Raketenprinzip Satelliten Rückstoßprinzip Verbrennungstriebwerke Impulserhaltungssatz Raketenkörper Düsen Differentialgleichung thermonukleares Triebwerk Dampftriebwerk innere Kräfte
Ein Angebot von 