Schiefer elastischer Stoß

Stößt ein Körper, z.B. eine Billardkugel, unter einem beliebigen Winkel ungleich 0° und ungleich 90° gegen eine Wand, so spricht man von einem schiefen elastischen Stoß. Das Gegenstück wäre ein gerader Stoß. Für einen solchen schiefen Stoß gilt der Impulserhaltungssatz und der Energieerhaltungssatz der Mechanik. Die Reflexion an einer festen Wand ist sehr kompliziert, wenn man Drehungen mit beachtet. Bei Annahme eines Massepunktes erfolgt die Reflexion entsprechend dem Reflexionsgesetz.

Reflexion

#Optik #Lichtbrechung #Reflexion #Licht an Grenzflächen #Reflexionsgesetz

Beispiele für solche schiefen elastischen Stöße sind der Stoß einer Billardkugel gegen die Bande oder das schiefe Auftreffen eines hochelastischen Balles auf dem Boden.

Für einen solchen schiefen elastischen Stoß gelten wie für alle elastischen Stöße der Impulserhaltungssatz und der Energieerhaltungssatz der Mechanik. Dabei sind allerdings zwei Fälle zu unterscheiden:

Betrachtet man reale Körper, z.B. eine Billardkugel oder einen Ball, so ist der schiefe Stoß immer mit Drehungen des betreffenden Körpers verbunden. Dadurch werden die Verhältnisse sehr kompliziert und lassen sich mathematisch in elementarer Form nicht mehr erfassen.
Betrachtet man den Körper als Massepunkt und schließt man die Rotation aus, dann ist eine mathematische Erfassung mithilfe der Erhaltungssätze möglich. Wir beschränken uns auf diesen Fall.

Schiefer elastischer Stoß eines Massepunktes

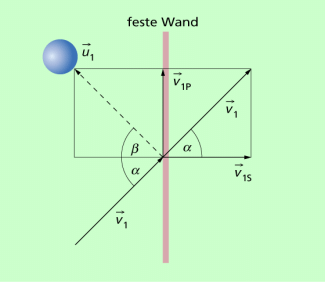
Wir betrachten den in Bild 2 dargestellten Fall des Stoßes eines Massepunktes gegen eine feste Wand. Dazu denkt man sich die Geschwindigkeit vor dem Stoß, ${\vec{v}}_{1}$ , in zwei Komponenten zerlegt, eine parallel und eine senkrecht zur Wand ( ${\vec{v}}_{1 S} und {\vec{v}}_{1 P}$ ) .Beim elastischen Stoß ändert sich ${\vec{v}}_{1 P}$ nicht. Die Geschwindigkeit nach dem Stoß hat also die identische Parallelkomponente:

${\vec{u}}_{1 P} = {\vec{v}}_{1 P}$

In Bezug auf die senkrechte Komponente erfährt die Kugel einen zentralen elastischen Stoß. Da die Wand sich nicht bewegt, gilt:

${\vec{u}}_{1 S} = - {\vec{v}}_{1 S}$

Bild 2 zeigt die Geometrie. Man liest direkt ab:
$α = β$
Der Einfallswinkel ist gleich dem Ausfallswinkel (Reflexionswinkel), wie bei der Reflexion von Licht. Es gilt also für einen Massepunkt das Reflexionsgesetz.

Geschwindigkeiten beim schiefen elastischen Stoß gegen eine Wand

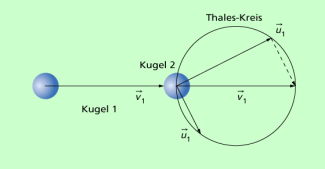
Schiefer elastischer Stoß zwischen Körpern gleicher Masse

Bild 3 zeigt den Stoß zwischen zwei gleich schweren Kugeln. Kugel 2 sei vor dem Stoß in Ruhe. Aus dem Energieerhaltungssatz folgt:
$\begin{array}{l} \frac{1}{2} m \cdot v_{1}^{2} = \frac{1}{2} m \cdot u_{1}^{2} + \frac{1}{2} m \cdot u_{2}^{2} \\ oder \\ v_{1}^{2} = u_{1}^{2} + u_{2}^{2} \end{array}$
Beim zentralen Stoß ist:
${\vec{u}}_{1} = 0 und {\vec{u}}_{2} = {\vec{v}}_{1}$
Die zweite Kugel bewegt sich in der gleichen Richtung weiter.

Ist der Stoß nicht zentral, treten Winkel zwischen $u_{1} und u_{2}$ auf. Stets aber bilden ${\vec{u}}_{1}, {\vec{u}}_{2} und {\vec{v}}_{1}$ die Seiten eines rechtwinkligen Dreiecks mit der Hypotenusenlänge ${\vec{v}}_{1}$ (Bild 3).
Die dargestellten Zusammenhänge werden z.B. genutzt, um Nebelkammeraufnahmen auszuwerten.

Schiefer elastischer Stoß zwischen zwei Kugeln gleicher Masse

Lernprobleme in Physik?

Mit deinem persönlichen Nachhilfe-Tutor Kim & Duden Learnattack checkst du alles. Jetzt 30 Tage risikofrei testen.

KI-Tutor Kim hilft bei allen schulischen Problemen
Individuelle, kindgerechte Förderung in Dialogform
Lernplattform für 9 Fächer ab der 4. Klasse
Über 40.000 Erklärvideos, Übungen & Klassenarbeiten
Rund um die Uhr für dich da

Jetzt in Physik durchstarten

Verwandte Artikel

Angaben zum Lexikon

Impressum

Schiefer elastischer Stoß

Reflexion

Schiefer elastischer Stoß eines Massepunktes

Schiefer elastischer Stoß zwischen Körpern gleicher Masse

Rechtliches

Einloggen