Volumen von Körpern

Das Volumen (der Rauminhalt) gibt an, wie viel Raum ein Körper einnimmt.

Formelzeichen:
Einheiten:

V
1 Kubikmeter (1

m^{3}

)
1 Liter (1 l)

Spezielle Volumeneinheiten sind ein Barrel (1 barrel) und eine Bruttoregistertonne (1 BRT). Das Volumen kann berechnet, mit Messzylindern oder Durchflusszählern direkt gemessen oder experimentell ermittelt werden.

Beziehungen zwischen den Einheiten

Teile der Einheit 1 $m^{3}$ sind ein Kubikdezimeter ( 1 $d m^{3}$ ), ein Kubikzentimeter (1 $c m^{3}$ ) und ein Kubikmillimeter (1 $m m^{3}$ ):

1 $m^{3}$ = 1 000 $d m^{3}$ = 1 000 000 $c m^{3}$ = 1 000 000 000 $m m^{3}$
1 $d m^{3}$ = 1 000 $c m^{3}$ = 1 000 000 $m m^{3}$
1 $c m^{3}$ = 1 000 $m m^{3}$

Vielfache und Teile der Einheit 1 l sind ein Hektoliter (1 hl) und
ein Milliliter (1 ml):

1 hl = 100 l
1 l = 1 000 ml

Zwischen den Einheiten bestehen folgende Beziehungen:

1 $m^{3}$ = 1 000 l
1 $d m^{3}$ = 1 l
1 $c m^{3}$ = 1 ml

Das Volumen von Erdöl wird häufig in Barrel (barrel) angegeben:
1 barrel = 158,758 l
Der Rauminhalt von Schiffen wird in Registertonnen bzw. Bruttoregistertonnen (BRT) angegeben:

1 Registertonne = 2,83 $m^{3}$

Volumen von Körpern in Natur und Technik

Nachfolgend ist das Volumen einiger Körper aus Natur und Technik angegeben.

Ameise	ca. 2 $m m^{3}$
Wassertropfen	0,3 ml
Tischtennisball	25 cm
Streichholzschachtel	28 cm
große Tasse	0,25 l
Limonadenflasche	0,75 l oder 1 l
Mauerziegel	2,2 $d m^{3}$
Ball (20 cm Durchmesser)	4,2 $d m^{3}$
Wassereimer	10 l
Tank eines PKW	45 l bis 60 l
Spermüllcontainer	6 $m^{3}$
Klassenzimmer	250 $m^{3}$
Tankwagen	20000 l
Öltanker	bis 500000 l
Cheopspyramide in Ägypten	2500000 $m^{3}$
Mond der Erde	$2,1991 \cdot 10^{19} m^{3}$
Erde	$1,0832 \cdot 10^{21} m^{3}$

Volumenänderung von Körpern - Zähler

L. Meyer, Potsdam

Messen des Volumens

Das Volumen von strömenden Flüssigkeiten und Gasen wird mit Durchflusszählern (Wasseruhr, Gasuhr) gemessen (Bild 1).
Das Volumen von pulverförmigen festen Körpern (z. B. Mehl, Zucker) und von ruhenden Flüssigkeiten wird mit Messbechern bzw. mit Messzylindern gemessen (Bild 2).

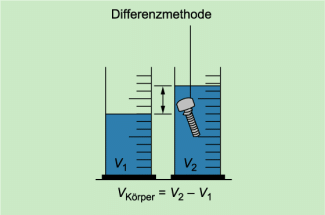
Das Volumen von unregelmäßig geformten festen Körpern kann mithilfe von Messzylindern bestimmt werden. Dabei nutzt man die Differenzmethode oder die Überlaufmethode.
Bei der Differenzmethode (Bild 3) befindet sich Wasser mit dem Volumen 1 in einem Messzylinder. Taucht man den Körper vollständig ein, so wird Wasser verdrängt. Man erhält das Volumen 2 (Bild 3). Die Differenz aus den beiden Volumen ist gleich dem Volumen des eingetauchten Körpers.

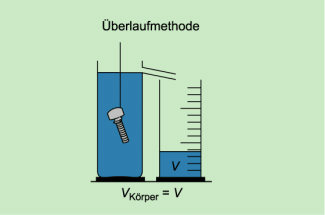
Bei der Überlaufmethode (Bild 4) ist ein Gefäß mit einem Überlauf randvoll mit Wasser gefüllt. Wird ein Körper vollständig in die Flüssigkeit eingetaucht, so läuft genau so viel Wasser in den Messzylinder, wie der Körper verdrängt. Das Volumen des Wassers im Messzylinder ist gleich dem Volumen des eingetauchten Körpers.

Vorgehen beim Messen mit einem Messzylinder

Beim Messen mit einem Messzylinder sollte man folgendermaßen vorgehen:

Schätzen Sie zunächst das Volumen des betreffenden Körpers und wählen Sie einen geeigneten Messzylinder aus!
Füllen Sie die Flüssigkeit in den Messzylinder! Stellen Sie ihn auf eine waagerechte Unterlage!
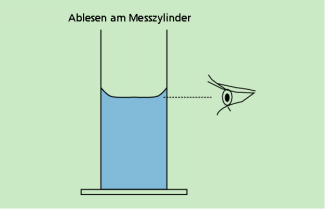
Lesen Sie den Stand an der tiefsten Stelle der Oberfläche ab! Schauen Sie dabei waagerecht auf die Oberfläche (Bild 5)!

Berechnen des Volumens aus den Abmessungen des Körpers

Das Volumen regelmäßig geformter fester Körper kann aus seinen Abmessungen berechnet werden.

Bei Würfeln gilt: $V = a \cdot a \cdot a$

Bei Quadern gilt: $V = a \cdot b \cdot c$

Für eine Kugel gilt: $V = \frac{4}{3} π \cdot r^{3}$

Für einen geraden Kreiszylinder gilt: $V = π \cdot r^{2} \cdot h$

Für einen geraden Kreiskegel gilt: $V = \frac{1}{3} π \cdot r^{2} \cdot h$

Für eine quadratische Pyramide gilt: $V = \frac{1}{3} a^{2} \cdot h$

Berechnung des Volumens aus Masse und Dichte

Sind Masse und Dichte eines Körpers bekannt, so kann sein Volumen mit folgender Gleichung berechnet werden:

$\begin{array}{l} V = \frac{m}{ρ} \\ m Masse des Körpers \\ ρ Dichte des Stoffes, aus dem der Körper besteht \end{array}$

Berechnung des Volumens von Rotationskörpern

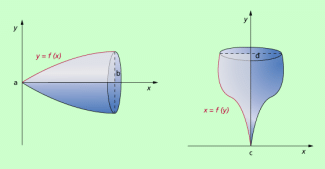
Für Rotationskörper kann man das Volumen auch mithilfe der Integralrechnung bestimmen. Das ist mitunter für die Berechnung des Trägheitsmomentes von Körpern wichtig. Erforderlich ist dabei allerdings die Kenntnis der Gleichung für den Graphen der Funktion, durch den die Fläche begrenzt wird.
Für einen Rotationskörper um die x-Achse (Bild 6a) gilt:

$V_{x} = π \int_{a}^{b} y^{2} d x = π \int_{a}^{b} {[f (x)]}^{2} d x$

Für einen Rotationskörper um die y-Achse (Bild 6b) gilt:

$V_{y} = π \int_{c}^{d} x^{2} dy = π \int_{c}^{d} {[f (y)]}^{2} dy$

Stand: 2010
Dieser Text befindet sich in redaktioneller Bearbeitung.

Lernprobleme in Physik?

Mit deinem persönlichen Nachhilfe-Tutor Kim & Duden Learnattack checkst du alles. Jetzt 30 Tage risikofrei testen.

KI-Tutor Kim hilft bei allen schulischen Problemen
Individuelle, kindgerechte Förderung in Dialogform
Lernplattform für 9 Fächer ab der 4. Klasse
Über 40.000 Erklärvideos, Übungen & Klassenarbeiten
Rund um die Uhr für dich da

Jetzt in Physik durchstarten

Verwandte Artikel

Angaben zum Lexikon

Impressum