- Lexikon
- Physik
- 2 Mechanik
- 2.5 Mechanische Schwingungen und Wellen
- 2.5.2 Mechanische Wellen
- Beschreibung mechanischer Wellen
Beschreibung mechanischer Wellen
Eine mechanische Welle ist die Ausbreitung einer mechanischen Schwingung im Raum. Beispiele für mechanische Wellen sind Wasserwellen, Schallwellen oder Erdbebenwellen. Für die Beschreibung mechanischer Wellen gibt es unterschiedliche Möglichkeiten, die nachfolgend im Einzelnen dargestellt sind.
Diese Beschreibungen mechanischer Wellen gelten für alle Arten von Wellen. In der Physik unterscheidet man zwischen folgenden zwei Arten:
- Querwellen oder Transversalwellen sind dadurch gekennzeichnet, dass die Schwingungsrichtung der einzelnen Teilchen stets senkrecht zur Ausbreitungsrichtung der Welle erfolgt. Solche Querwellen treten z. B. bei Erdbeben auf und lassen sich einfach als Seilwellen demonstrieren (Simulation 1).
- Längswellen oder Longitudinalwellen sind dadurch gekennzeichnet, dass die Schwingungsrichtung der einzelnen Teilchen in Richtung der Ausbreitungsrichtung erfolgt. Ein Beispiel für solche Längswellen sind Schallwellen (Simulation 2).
- Eine spezielle Art von Querwellen sind Kreiswellen, die wir als Wasserwellen beobachten können. Bei solchen Kreiswellen bewegen sich die Wasserteilchen auf kreisförmigen Bahnen. die Gesamtheit der Wasserteilchen ergibt eine Welle, die sich im Raum ausbreitet (Simulation 3).
Beschreibung mechanischer Wellen mit Diagrammen
Ähnlich wie mechanische Schwingungen lassen sich mechanische Wellen durch Diagramme beschreiben.
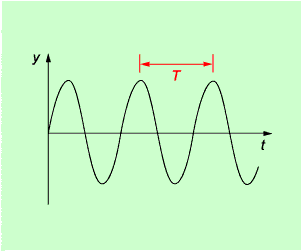
Wird für einen bestimmten Ort x (x = konstant) dargestellt, wie sich der Schwinger an diesem Ort in Abhängigkeit von der Zeit bewegt, so erhält man wie bei einer Schwingung ein y-t-Diagramm. y ist dabei die Auslenkung (Elongation), t die Zeit (Bild 2).
Beschrieben wird mit diesem Diagramm die Bewegung eines Schwingers. Abgelesen werden kann aus dem y-t-Diagramm die Auslenkung (Elongation) y zu verschiedenen Zeiten t. Der Abstand zweier benachbarter Wellenberge ist gleich der Schwingungsdauer (Periodendauer) T des Schwingers.
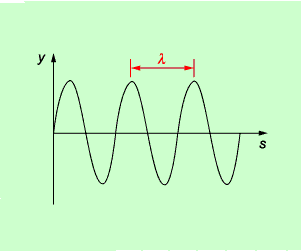
Wird für einen bestimmten Zeitpunkt t (t = konstant) dargestellt, welche Lage die einzelnen Schwinger zu diesem Zeitpunkt haben, so erhält man ein y-x-Diagramm. y ist dabei wieder die Auslenkung (Elongation), x der Ort des jeweiligen Schwingers (Bild 3). Statt des Ortes x verwendet man zur Beschreibung manchmal auch den Weg s.
Beschrieben wird mit diesem Diagramm der jeweilige Schwingungszustand vieler Schwinger zu einem bestimmten Zeitpunkt. Man hat also eine "Momentaufnahme" einer Welle vor sich.
Abgelesen werden kann aus dem y-x-Diagramm die momentane Auslenkung y eines Schwingers an einem bestimmten Ort x, wobei man x (oder s) von einem (willkürlich) gewählten Nullpunkt aus misst. Der Abstand zweier benachbarter Wellenberge ist gleich der Wellenlänge.
Beschreibung mechanischer Wellen mit physikalischen Größen
Da bei einer Welle jeder einzelne Körper bzw. jedes Teilchen mechanische Schwingungen ausführt, können zur Beschreibung von Wellen zunächst solche physikalischen Größen genutzt werden, die man auch zur Beschreibung von Schwingungen verwendet. Es handelt sich dabei um die Auslenkung (Elongation), die Amplitude , die Schwingungsdauer (Periodendauer) und die Frequenz .
Darüber hinaus wird eine mechanische Welle mit den physikalischen Größen Wellenlänge und Ausbreitungsgeschwindigkeit beschrieben.
Es gilt:
Die Wellenlänge einer Welle gibt den Abstand zweier benachbarter Schwinger an, die sich im gleichen Schwingungszustand befinden.
| Formelzeichen: | |||
| Einheit: | ein Meter (1 m) |
Gleiche Schwingungszustände sind z. B. zwei benachbarte Wellenberge oder zwei Wellentäler. Ihr Abstand voneinander ist gleich der Wellenlänge (Bild 3).
Die Ausbreitungsgeschwindigkeit einer Welle ist die Geschwindigkeit, mit der sich ein Schwingungszustand im Raum ausbreitet.
| Formelzeichen: | v oder c | ||
| Einheit: | ein Meter je Sekunde (1 m/s) |
Messen kann man die Ausbreitungsgeschwindigkeit z. B. so, dass man bestimmt, wie schnell sich ein Wellenberg ausbreitet.
In der nachfolgenden Übersicht werden Wellenlängen und Ausbreitungsgeschwindigkeiten für einige mechanische Wellen angegeben.
Zwischen der Ausbreitungsgeschwindigkeit einer Welle, ihrer Wellenlänge und der Frequenz besteht ein enger Zusammenhang.
Für alle mechanische Wellen gilt:
Breitet sich eine Welle in einem Stoff mit gleicher Dichte und bestimmter Temperatur aus, so bleibt die Ausbreitungsgeschwindigkeit konstant. Für v = konstant gilt:
Das bedeutet: Je größer die Wellenlänge ist, desto kleiner ist die Frequenz. Je kleiner die Wellenlänge ist, desto größer ist die Frequenz.
Geht eine mechanische Welle von einem Stoff in einen anderen über, z. B. Schallwellen von Luft in Wasser, dann bleibt die Frequenz stets gleich. Es ändert sich aber im Allgemeinen die Ausbreitungsgeschwindigkeit und damit die Wellenlänge, da für
f = konstant gilt:
Das bedeutet: Mit Vergrößerung der Ausbreitungsgeschwindigkeit vergrößert sich die Wellenlänge, mit Verkleinerung der Ausbreitungsgeschwindigkeit verkleinert sie sich.
Beschreibung mit der Wellengleichung
Eine mechanische Welle kann auch mit einer Gleichung beschrieben werden. Dabei wird vorausgesetzt, dass die einzelnen Schwinger eine harmonische Schwingung ausführen und damit die Bewegung des einzelnen Schwingers mit der Sinus-Funktion beschrieben werden kann.
Unter der Bedingung, dass die einzelnen Schwinger harmonische (sinusförmige) Schwingungen ausführen, gilt die Wellengleichung . Sie lautet:
Berechnungstool Ausbreitungsgeschwindigkeit Transversalwelle Wellenlänge y-x-Diagramm Seilwellen harmonische Schwingung Amplitude y-t-Diagramm Querwelle Längswelle Kreiswelle Wellengleichung Periodendauer Longitudinalwelle Auslenkung Beschreibung mechanischer Wellen Elongation Frequenz mechanische Wellen Simulation y-s-diagramm Schallwelle Schwingungsdauer Animation
Stand: 2010
Dieser Text befindet sich in redaktioneller Bearbeitung.
Ein Angebot von 