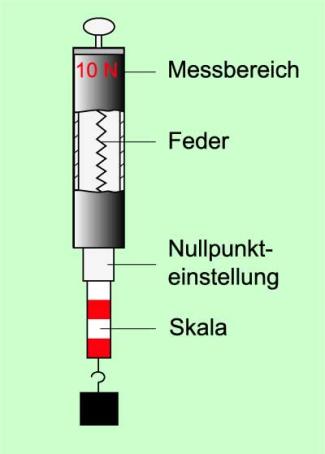
Federkraftmesser

Federkraftmesser sind Messgeräte zur Messung der physikalischen Größe Kraft. Bei ihnen wird das hookesche Gesetz genutzt, das besagt: Bei einer elastisch verformten Feder ist die Ausdehnung proportional zur einwirkenden Kraft. Es gilt:

$s~F$

Ein Federkraftmesser besteht aus einer elastischen Feder, eine Skala und einer Nullpunkteinstellung (Bild 2). Wird an die Feder ein Körper angehängt, so dehnt sich die Feder aus. Die Dehnung der Feder ist umso größer, je größer die einwirkende Kraft ist. Somit ist die Dehnung der Feder ein Maß für den Betrag der wirkenden Kraft, die direkt an der Skala in der Einheit Newton abgelesen werden kann.

Der Messbereich eines Federkraftmessers hängt von der Art der eingebauten Feder ab. Je härter die Feder ist, umso größer ist der Messbereich des Federkraftmessers. Gekennzeichnet wird die Härte einer Feder durch die Federkonstante D, für die gilt (hookesches Gesetz):

$D=\frac{F}{s}$

Die Federkonstante einer Feder kann man ermitteln, indem man auf eine Feder eine bestimmte Kraft einwirken lässt und die Dehnung der Feder durch diese Kraft bestimmt. Der Betrag der Federkonstanten wird in N/cm oder in N/m angegeben.

Die Messgenauigkeit eines Federkraftmessers hängt im Wesentlichen von der Art der Feder (Federkonstanten) und von der Skaleneinteilung ab.

Beim Messen mit einem Federkraftmesser sollte man folgendermaßen vorgehen:

1. Wähle einen geeigneten Federkraftmesser aus! Beachte dabei den Messbereich!
2. Stelle mithilfe der Nullpunkteinstellung den Nullpunkt ein! Beachte, dass dabei der Federkraftmesser senkrecht hängen muss!
3. Lass die Kraft einwirken und lies an der Skala den Betrag der Kraft ab! Schaue dabei waagerecht auf die Skala!