- Lexikon
- Physik
- 2 Mechanik
- 2.4 Mechanische Arbeit, Energie und Leistung
- 2.4.2 Die mechanische Energie
- Potenzielle Energie
Potenzielle Energie
Gehobene Körper, z. B. eine an einem Kranhaken hängende Betonplatte, Kletterer oder Kinder auf dem Ast, besitzen potenzielle Energie. Ebenfalls potenzielle Energie haben eine gespannte Feder, ein verbogener Ast oder der gebogene Sprungstab eines Stabhochspringers. Statt von potenzieller Energie spricht man auch von Energie der Lage oder Lageenergie. Allgemein gilt:
Potenzielle Energie ist die Fähigkeit eines Körpers, aufgrund seiner Lage mechanische Arbeit zu verrichten, Wärme abzugeben oder Licht auszusenden.
| Formelzeichen: Einheiten: | ein Joule (1 J) ein Newtonmeter (1 Nm) |
Potenzielle Energie ist eine spezielle Form mechanischer Energie. Die andere Form mechanischer Energie ist die kinetische Energie. Die potenzielle Energie kennzeichnet den Zustand eines gehobenen oder eines verformten Körpers und wird deshalb wie jede Form von Energie auch als Zustandsgröße bezeichnet. Potenzielle Energie kann in einem Körper gespeichert sein. Sie kann auch in andere Energieformen umgewandelt oder von einem Körper auf andere Körper übertragen werden.
Berechnung potenzieller Energie
Die potenzielle Energie eines gehobenen Körpers hängt von seiner Masse bzw. seiner Gewichtskraft sowie davon ab, in welcher Höhe er sich befindet. Sie ist umso größer,
- je größer die Gewichtskraft des Körper ist und
- je höher er sich befindet.
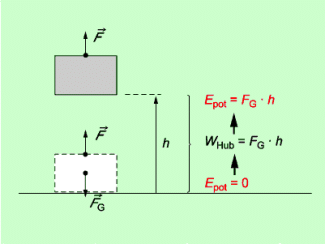
Die potenzielle Energie eines gehobenen Körpers kann berechnet werden mit den Gleichungen:
Sie ist genau so groß wie die Hubarbeit, die zum Heben des Körpers in die Höhe h erforderlich ist (Bild 2). Dabei ist zu beachten, dass man die Höhe h stets auf eine bestimmte Ausgangshöhe null beziehen muss. Was man als Ausgangshöhe wählt, hängt häufig von der Zweckmäßigkeit ab.
Für einen Körper, der auf einem Tisch der Höhe h steht, kann man als Ausgangshöhe z. B. die Tischoberfläche oder auch den Fußboden wählen. Im ersten Fall ist die potenzielle Energie des Körpers null, weil h = 0 ist. Im zweiten Fall ist die potenzielle Energie des Körpers größer als null, weil er sich in einer bestimmten Höhe über dem Fußboden befindet.
Die potenzielle Energie einer gespannten Feder hängt von der Härte der Feder und davon ab, wie weit sie gedehnt ist. Sie ist umso größer,
- je härter die Feder und damit je größer die Federkonstante ist und
- je stärker die Feder gedehnt wird.
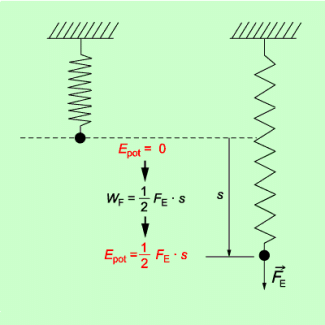
Die potenzielle Energie einer gespannten Feder kann berechnet werden mit den Gleichungen:
Sie ist genau so groß wie die zuvor an ihr verrichtete Verformungsarbeit (Federspannarbeit).
In der nachfolgenden Übersicht sind einige Werte für die potenzielle Energie von Körpern in Natur und Technik angegeben.
Potenzielle Energie in Natur und Technik | |
| Feder (D = 0,2 N/cm), um 10 cm gedehnt | 0,01 J |
| Tafel Schokolade (m = 100 g), um 1 m gehoben | 1 J |
| Ziegelstein (m = 3,5 kg), um 1 m gehoben | 35 J |
| Mensch (m = 55 kg) auf 10-m-Sprungturm | 5 500 J = 5,5 kJ |
| Rammbär (m = 1 000 kg), um 1 m gehoben | 10 000 J = 10 kJ |
| Flugzeug (m = 100 t) in 1 km Höhe | |
Ein Angebot von 