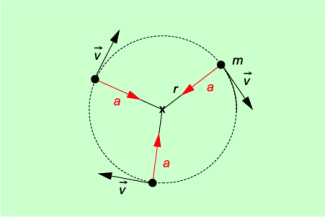
Radialbeschleunigung

Die Radialbeschleunigung gibt an, wie schnell sich bei einer Kreisbewegung die Geschwindigkeit ändert.
Formelzeichen: $a_r$
Einheit: ein Meter je Quadratsekunde $(1\frac{\text{m}}{{\text{s}}^{\text{2}}})$
Die Radialbeschleunigung kann mit den folgenden Gleichungen berechnet werden:

$a_r=\frac{v^2}{r}{a}_r=\frac{4{\pi }^2\cdot r}{T^2}{a}_r=4{\pi }^2\cdot r\cdot n^2$

Die Radialbeschleunigung ist eine gerichtete (vektorielle) Größe, die immer zum Zentrum der Kreisbewegung gerichtet ist. Sie ist deutlich zu unterscheiden von einer Beschleunigung längs der Bahn des Körpers (Bahnbeschleunigung oder Beschleunigung).
Kennt man die Radialbeschleunigung für einen Körper, so kann man auch die Radialkraft bestimmen. Umgekehrt kann man bei bekannter Masse des Körpers aus der Radialkraft die Radialbeschleunigung ermitteln. Dabei wird das newtonsche Grundgesetz angewendet. Setzt man in die Gleichung

$F=m\cdot a$

für die Beschleunigung a die Radialbeschleunigung ein, so erhält man die Gleichungen für die Radialkraft:

$F_r=m\cdot \frac{v^2}{r}{F}_r=m\cdot \frac{4{\pi }^2\cdot r}{T^2}{F}_r=m\cdot 4{\pi }^2\cdot r\cdot n^2$