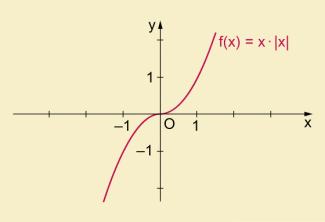Betragsfunktion

Die formale Definition des absoluten Betrages (Absolutbetrags) einer reellen Zahl x ist die folgende:

$f\left(x\right)=\left|x\right|=\{\begin{array}{c}x,\text{falls }x\ge 0\\ -x,\text{falls }x<0\end{array}$

Aus dieser Definition folgt, dass immer $\left|x\right|\ge 0$ gilt.

Weiter ist Null die einzige Zahl, für die der Absolutbetrag gleich null ist. Das kann kurz und bündig folgendermaßen formuliert werden:
$\left|x\right|=0\iff x=0$

Der Absolutbetrag erkennt die „Größe“ einer Zahl, ohne dabei auf das Vorzeichen zu achten. Die Tatsache, dass er das Vorzeichen ignoriert, lässt sich mathematisch als $\left|x\right|=\left|-x\right|$ schreiben.

Auf der Zahlengeraden ist der Absolutbetrag der (stets nicht negative) Abstand einer Zahl vom Nullpunkt. Eine Größe $\left|\mathrm{17,3}-\mathrm{19,3}\right|$ stellt den (positiv genommenen) Abstand zwischen den beiden Punkten 17,3 und 19,3 auf der Zahlengeraden dar (welcher sich als 2 erweist). Diese Bezeichnungsweise ist wichtig, wenn von zwei Zahlen gesagt werden soll, dass sie nahe beieinander liegen (wobei egal sein soll, welche die größere ist). Das Bequeme daran ist, dass man dabei nicht auf die Reihenfolge achten muss, da immer die folgende Beziehung gilt:
$\left|x-y\right|=\left|y-x\right|$
(was aus $\left|x\right|=\left|-x\right|$ folgt)

Sind die beiden Punkte x und y voneinander verschieden und liegen nahe beieinander, so ist $\left|x-y\right|$ klein (und positiv). Sind die Punkte gleich, so ist $\left|x-y\right|=0$. Diese Eigenschaft des Absolutbetrags verwenden wir in der Mathematik sehr oft.

Im Folgenden sollen wesentliche Eigenschaften des Absolutbetrags angeführt werden. Für alle reellen Zahlen a und b gilt:

1. $\left|a\right|=\left|-a\right|$
2. $\left|a\right|\ge 0;\left|a\right|=0\iff a=0$
3. $\left|a\cdot b\right|=\left|a\right|\cdot \left|b\right|$
4. $\left|\frac{a}{b}\right|=\frac{\left|a\right|}{\left|b\right|}füralleb\ne 0$
5. $\left|a^n\right|={\left|a\right|}^{n}fürn\in \mathbb{N}$
6. $-\left|a\right|\le a\le \left|a\right|$
7. $\left|a\pm b\right|\le \left|a\right|+\left|b\right|$ (Dreiecksungleichung)
8. $\left|a\right|-\left|b\right|\le \left|\left|a\right|-\left|b\right|\right|\le \left|a\pm b\right|\le \left|a\right|+\left|b\right|$
9. $\left|a\right|\le b\Rightarrow -b\le a\le b$
10. $\left|a\right|\ge b\Rightarrow (entweder)a\le -bodera\ge b$
11. $\left|a\right|\le \left|b\right|\Rightarrow a^2\le b^2$
12. $\sqrt{a^2}=\left|a\right|;\sqrt[2k]{a^{2k}}=\left|a\right|fürk\in N$

Es ist klar, dass für jede reelle Zahl a gilt:
$\left|a\right|\ge aund\left|a\right|\ge -a$

Wir beweisen nun die folgende Aussage (Dreiecksungleichung):
$\left|a+b\right|\le \left|a\right|+\left|b\right|$

1. Fall: Sei $a+b\ge 0$.
Dann erhalten wir $\left|a+b\right|=a+b$ und wegen $b\le \left|b\right|,a\le \left|a\right|$ unmittelbar $\left|a+b\right|=a+b\le \left|a\right|+\left|b\right|$.

2. Fall: Sei $a+b<0$.
Mit $\left|a\right|\ge -aund\left|b\right|\ge -b$ erhalten wir dann $\left|a+b\right|=-\left(a+b\right)=-a-b\le \left|a\right|+\left|b\right|$.

Leicht zu zeigen ist auch Folgendes:
Wenn $\left|a\right|\le Aund\left|b\right|\le B$, dann $\left|a+b\right|\le A+Bund\left|ab\right|\le AB$.

Rechnen mit Beträgen

• Beispiel 1: Berechnen Sie $\sqrt{14-8\sqrt{3}}$
  Lösung:
  $\begin{array}{l}\sqrt{14-8\sqrt{3}}=\sqrt{6-2\cdot 4\sqrt{3}+8}=\sqrt{6-2\sqrt{48}+8}\\ =\sqrt{{\left(\sqrt{6}-\sqrt{8}\right)}^2}=\left|\sqrt{6}-\sqrt{8}\right|=\sqrt{8}-\sqrt{6}\end{array}$
• Beispiel 2: Beweisen Sie: $\sqrt{a^2+b^2+c^2}\le \left|a\right|+\left|b\right|+\left|c\right|$
  Lösung: Es ist klar, dass gilt:
  $\begin{array}{l}{a}^2+b^2+c^2\le a^2+b^2+c^2+2\left|a\right|\left|b\right|+2\left|a\right|\left|c\right|+2\left|b\right|\left|c\right|\\ ={\left(\left|a\right|+\left|b\right|+\left|c\right|\right)}^2\end{array}$
  Daraus folgt sofort $\sqrt{a^2+b^2+c^2}\le \left|a\right|+\left|b\right|+\left|c\right|$.
• Beispiel 3: Zeigen Sie: $\underset{x\to 5}{\lim }\sqrt{x+4}=3$
  Lösung: Nach Definition des Grenzwertes muss es für alle $\epsilon >0$ ein $\delta >0$ geben mit
  $\left|x-5\right|<\delta \Rightarrow \left|\sqrt{x+4}-3\right|<\epsilon$
  Es ist
  $\begin{array}{l}\left|\sqrt{x+4}-3\right|=\left|\frac{\left(\sqrt{x+4}-3\right)\left(\sqrt{x+4}+3\right)}{\sqrt{x+4}+3}\right|=\left|\frac{\left(x+4\right)-9}{\sqrt{x+4}+3}\right|\\ =\left|\frac{x-5}{\sqrt{x+4}+3}\right|\le \left|\frac{x-5}{+3}\right|<\epsilon \end{array}$
  Das heißt, für alle x mit $\left|x-5\right|<3\epsilon$ gilt $\left|\sqrt{x+4}-3\right|<\epsilon$, also $\delta =3\epsilon$und $\underset{x\to 5}{\lim }\sqrt{x+4}=3$.
• Beispiel 4: Lösen Sie nach x auf: $\sqrt[4]{{\left|x-3\right|}^{x+1}}=\sqrt[3]{{\left|x-3\right|}^{x-2}}$
  Lösung: Wir schreiben die Gleichung um:
  ${\left|x-3\right|}^{\frac{x+1}{4}}={\left|x-3\right|}^{\frac{x-2}{3}}$
  Sei $\left|x-3\right|=1$, dann ist $x-3=1oderx-3=-1$ und somit $x=4oderx=2$.
  Aus folgt $\left|x-3\right|=1$, $x=3$ und aus $\frac{x+1}{4}=\frac{x-2}{3}$ schließlich $x=11$. Wir erhalten also folgende Lösungsmenge:
  $L=\left\{2;3;4;11\right\}$

Betragsfunktion wird jene Funktion genannt, die jeder Zahl ihren Absolutbetrag zuordnet, d.h. $x\to \left|x\right|$. Sie ist ein Beispiel für eine Funktion, deren einfachste Definition nicht als Termdarstellung, sondern mit Hilfe einer Fallunterscheidung (s.o.) geschieht.

Im Folgenden werden einige weitere Beispiele grafischer Darstellungen von Funktionen mit Beträgen angegeben:

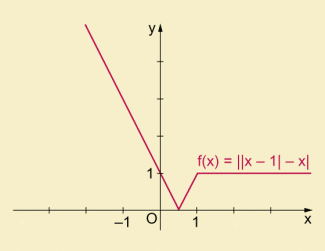
• Beispiel 5: $y=f\left(x\right)=\left|\left|x-1\right|-x\right|$
  Für $x\ge 1$ gilt: $y=\left|x-1-x\right|=\left|1\right|=1$
  Für $x<1$ gilt: $y=\left|1-x-x\right|=\left|1-2x\right|$

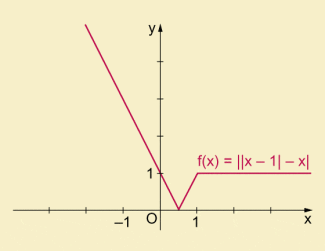
• Beispiel 6: $y=f\left(x\right)=x\cdot \left|x\right|$
  Es ist:
  $y=x\cdot \left|x\right|=\{\begin{array}{c}{x}^2,fallsx\ge 0\\ -x^2,fallsx<0\end{array}$

• Beispiel 7: $y=f\left(x\right)=\left|x^2-3x-4\right|$

Diese Funktion hat die gleichen Nullstellen wie $y=f\left(x\right)=x^2-3x-4$. Der Graph entsteht aus dem Graphen jener Funktion durch Spiegelung des unterhalb der x-Achse gelegenen Teiles an der Abszissenachse.