Die gaußsche Summenfunktion

Mit den vor allem im deutschsprachigen Raum benutzten Bezeichnungen für die Verteilungsfunktion der Standardnormalverteilung, die mit dem Namen des deutschen Mathematikers CARL FRIEDRICH GAUSS (1777 bis 1855) verbunden sind, werden dessen Verdienste um die sogenannte Fehlerrechnung gewürdigt. Dabei war es ihm gelungen, auf analytischem Wege die Gleichung für die nach ihm benannte Glockenkurve von $\varphi$ und damit auch für die Integralfunktion $\Phi$ herzuleiten.

Anhand des in der folgenden Abbildung dargestellten Graphen der Funktion $\Phi$ kann man sich die meisten ihrer nachfolgend angegebenen Eigenschaften verdeutlichen. Insbesondere gilt:

1. $\Phi \left(-a\right)=1-\Phi \left(a\right)fürallea\in ℝ$
2. $\Phi \left(0\right)=\mathrm{0,5};\Phi \left(-1\right)\approx \mathrm{0,16};\Phi \left(1\right)\approx \mathrm{0,84}$
   (wobei 0 der Erwartungswert und 1 der Wert der Standardabweichung von X ist)
3. Der Graph von $\Phi$ ist punktsymmetrisch zum Punkt $\left(0;\mathrm{0,5}\right)$.
4. Der Graph von $\Phi$ hat bei $x=0$ einen Wendepunkt.
5. Die Funktion $\Phi$ ist beliebig oft differenzierbar, und es gilt:${\Phi }^{\prime }=\varphi$
6. $\underset{a\to \infty }{\lim }\Phi \left(a\right)=1und\underset{a\to -\infty }{\lim }\Phi \left(a\right)=0$
7. $\Phi \left(a\right)>0fürallea\in ℝ$
8. Die Funktion $\Phi$ ist für alle $a\in ℝ$ streng monoton wachsend.

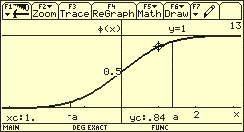
Die gaußsche Summenfunktion ist der gaußschen Glockenkurve in gewissem Sinne nachgeordnet. Das ergibt sich auch aus der Tatsache, dass für $\Phi$ keine analytisch geschlossene Funktionsgleichung existiert. In der Praxis begegnet einem allerdings die Normalverteilung oft zuerst nicht in Gestalt einer Glockenkurve, sondern als ein leicht S-förmiger, monoton wachsender Graph.

Beispiel: Auf einer Versuchsfläche wurden 125 Kiefern angepflanzt. Nach neun Jahren werden die Höhen, in Zentimeter aufgerundet, gemessen.
Daraus entstand das folgende Messprotokoll:

Ordnet man diese Werte der Größe nach und überträgt sie in ein Koordinatensystem, so erhält man den in der folgenden Abbildung dargestellten Verlauf.

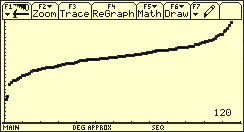
Anmerkung: Interaktiv können auch eigene Messprotokolle verwendet werden, z.B. zur zeitlichen Abfolge des Höhenwachstums einer Sonnenblume, zur Körpergröße aller Mädchen bzw. aller Jungen einer Klassenstufe, zum Wert einer bestimmten physikalischen Größe, die mehrmals durch verschiedene Schüler ermittelt wurde.

Das angenäherte Bild einer Glockenkurve entsteht häufig erst, wenn die „Urdaten“ in geeigneter Weise bearbeitet werden, indem man etwa bei den Kiefern zur Häufigkeitsverteilung der Kiefern in „20-cm-Intervalle“ übergeht (oder bei der Sonnenblume den von Woche zu Woche ermittelten Höhenzuwachs) betrachtet.

Die graphische Darstellung zur Größe der neunjährigen Kiefern lässt vermuten, dass eine Normalverteilung vorliegt, da bei der S-Kurve die mittleren Werte stark vertreten und Extreme selten sind. Dafür sprechen auch inhaltliche, durch den zentralen Grenzwertsatz gestützte Überlegungen.

Das Wachstum einer einzelnen Kiefer wird nämlich von einer Vielzahl unabhängig voneinander wirkender Faktoren beeinflusst, wie z.B. von der Qualität des Pflanzgutes, von der Art und Weise der Pflanzung, von der standortbedingten Bodenbeschaffenheit, vom standortabhängigen Einfluss von Wind, Sonne und Regen, vom Wirken verschiedener Tiere, Mikroorganismen und anderer Pflanzen usw., wobei von keinem dieser Faktoren ein dominierender Einfluss ausgeht.

Auch wenn die Normalverteilung in der Natur relativ häufig vorkommt, darf daraus nicht der Schluss gezogen werden, dass es dort nur normalverteilte Zufallsgrößen gäbe. Für die Verteilung der Lebensdauer von Lebewesen nutzt man z.B. das Modell der Exponentialverteilung.