Faktorregel der Differenzialrechnung

Der Differenzenquotient von f an der Stelle $x_0$ ist dann:

$\begin{array}{c}d\left(h\right)=\frac{k\cdot g\left(x_0+h\right)-k\cdot g\left(x_0\right)}{h}\\ =k\cdot \frac{g\left(x_0+h\right)-g\left(x_0\right)}{h}\left(mith\ne 0;x_0\in D_f\right)\end{array}$

Damit gilt für die Ableitung von f, da nach den Grenzwertsätzen für Funktionen der Grenzwert eines Produktes gleich dem Produkt der Grenzwerte seiner Faktoren (so diese existieren) ist:

$f^{\prime }\left(x_0\right)=\underset{h\to 0}{\lim }k\cdot \underset{h\to 0}{\lim }\frac{g\left(x_0+h\right)-g\left(x_0\right)}{h}=k\cdot g^{\prime }\left(x_0\right)$

und damit wegen der beliebigen Wahl von $x_0$

$f^{\prime }\left(x\right)=k\cdot g^{\prime }\left(x\right).$

Es gilt die Faktorregel der Differenzialrechnung:

• Ist g einen differenzierbare Funktion, so ist auch die Funktion f mit $f\left(x\right)=k\cdot g\left(x\right)\left(k\in ℝ\right)$ differenzierbar und es gilt $f^{\prime }\left(x\right)=k\cdot g^{\prime }\left(x\right)$.
  Mit anderen Worten:
  Ein konstanter Faktor bleibt beim Differenzieren erhalten – im Unterschied zu einem konstanten Summanden, dessen Ableitung gleich null ist.

Die Ableitung einer Funktion $f\left(x\right)=k\cdot g\left(x\right)$ und damit ihre Steigung an einer bestimmten Stelle $x_0$ ist also stets gleich dem k-fachen der Ableitung der Funktion g an dieser Stelle.

Das heißt: Der Graph der Funktion $f^{\prime }\left(x\right)=k\cdot g^{\prime }\left(x\right)$ geht aus dem Graphen von $g^{\prime }$ durch Streckung um das k-fache in y-Richtung hervor - in demselben Verhältnis, wie auch die Graphen von $f=k\cdot g$ und g zueinander stehen.

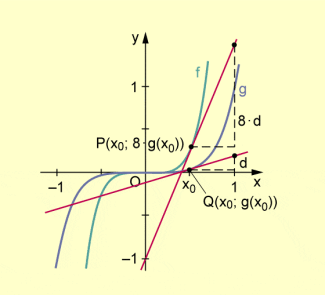
Der Graph der Funktionen f und g zeigt die Beziehungen zwischen den Funktionen f und g sowie die Beziehungen zwischen ihren Anstiegen an einer Stelle $x_0$ für $f=8\cdot g$.

An dieser Stelle gilt hier $f\left(x_0\right)=8\cdot g\left(x_0\right)$ und
$\text{Tangentenanstieg von }f=8\cdot \text{ Tangentenanstieg von }g$.