Kugel und Feder - Bewegungsgleichung oder Energiesatz

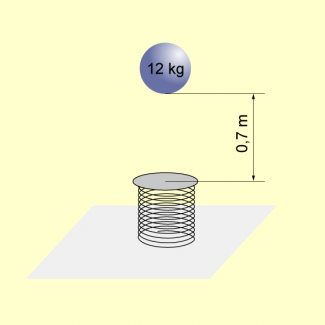
Beispiel: Ein Körper mit einer Masse von 12 kg fällt aus einer Höhe von 0,7 m auf eine Feder mit der Federkonstanten von $4000\frac{N}{m}$.
Es soll berechnet werden, um welches Stück die Feder beim Aufprall zusammengedrückt wird.

1. Berechnung mithilfe des newtonschen Grundgesetzes

Für die Aufschlaggeschwindigkeit gilt $v_0=\sqrt{2\cdot g\cdot h}.$

Im Folgenden versehen wir alle nach unten gerichteten Größen mit positivem Vorzeichen und umgekehrt. Dann können wir für die Kraft, die auf die Kugel wirkt bzw. für deren Beschleunigung schreiben:
$F=-D\cdot s+m\cdot g\text{bzw:}a=-\frac{D\cdot s}{m}+g$

Wenn wir $a=\frac{dv}{dt}$ schreiben, treten in der Gleichung drei Variable auf: v, s und t.
Um deren Zahl auf zwei zu reduzieren, die wir dann trennen können, schreiben wir $a=\frac{\text{d}v}{\text{d}t}=\frac{\text{d}v}{\text{d}x}\cdot \frac{\text{d}x}{\text{d}t}=\frac{\text{d}v}{\text{d}x}\cdot v=-\frac{D\cdot s}{m}+g$ und erhalten $v\cdot \text{d}v=\left(-\frac{D\cdot s}{m}+g\right)\cdot \text{d}s.$

Integration auf beiden Seiten ergibt:
$\frac{v^2}{2}=-\frac{D\cdot s^2}{2m}+g\cdot s+c$

Die Integrationskonstante c bestimmen wir aus der Anfangsbedingung ${\text{(für s = 0 ist v = v}}_{\text{0}}\text{) }$ zu$c=\frac{v_0^2}{2}$ und erhalten
$v=\sqrt{v_0^2+2\cdot g\cdot s-\frac{D\cdot s^2}{m}}=\sqrt{2\cdot g\cdot h+2\cdot g\cdot s-\frac{D\cdot s^2}{m}}.$

Damit haben wir für die gesamte Bewegung ab Aufschlag des Körpers die Geschwindigkeit in Abhängigkeit vom Ort berechnet, was die Aufgabe nicht verlangt.
Um zu berechnen, um welche Strecke die Feder zusammengedrückt wird, setzen wir $v=0$.

Das führt auf die quadratische Gleichung
$s^2-\frac{2\cdot g\cdot m}{D}\cdot s-\frac{2\cdot g\cdot m\cdot h}{D}=0$
mit der einzigen positiven Lösung s = 0,235 m.

2. Berechnung mittels Energiesatz

$\begin{array}{l}AbnahmeZunahme\\ derpotentielleEnergie=derSpannenergie\\ desKörpersderFeder\\ m\cdot g\cdot \left(h+s\right)=\frac{1}{2}\cdot D\cdot s^2\end{array}$

Daraus erhält man nach kurzer Rechnung dieselbe quadratische Gleichung wie oben.

Wir sehen, dass die Berechnung mit dem Energiesatz wesentlich einfacher und kürzer ist, sie liefert aber auch weniger Information. Für viele Probleme in der Mechanik gibt es diese beiden Vorgehensweisen.