Ebenes Koordinatensystem

Koordinatensysteme sind unentbehrliche Hilfsmittel, wenn man geometrische Probleme mit rechnerischen Mitteln lösen will oder umgekehrt die Resultate geometrisch interpretieren möchte, die sich bei der Behandlung bestimmter Probleme mit rechnerischen Methoden ergeben haben. Koordinatensysteme sind in diesem Sinne gleichsam Bindeglieder zwischen Geometrie und Arithmetik, die es überdies vielfach überhaupt erst ermöglichen, bestimmte praktische, „außermathematische“ Sachverhalte einer mathematischen Bearbeitung zugänglich zu machen, sie mathematisch zu „modellieren“.

Ein Koordinatensystem der Ebene besteht aus zwei einander im Nullpunkt – dem Koordinatenursprung O – schneidenden Zahlengeraden, wobei man die eine Gerade als Abszissenachse (in der Regel auch x-Achse), die andere als Ordinatenachse (in der Regel auch y-Achse) bezeichnet. Auf jeder Achse ist ein von O verschiedener Koordinateneinheitspunkt festgelegt.

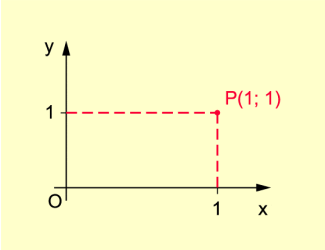
Stehen die beiden Achsen senkrecht aufeinander, so bilden sie ein rechtwinkliges Koordinatensystem (Bild 1).

Ein kartesisches Koordinatensystem liegt vor, wenn bei einem rechtwinkligen Koordinatensystem außerdem die Einheitsstrecken auf beiden Achsen gleich lang sind.

Dabei ist festgelegt, dass die gerichtete x-Achse bei Drehung entgegen dem Uhrzeigersinn (also im mathematisch positiven Drehsinn) auf kürzestem Weg in die gerichtete y-Achse übergeht. Man sagt dann: Die x- und die y-Achse bilden ein Rechtssystem.
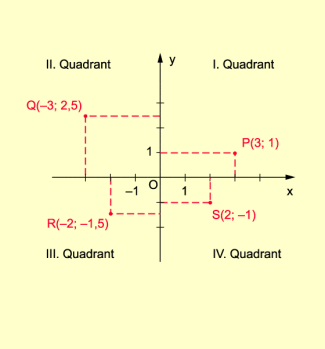
Mithilfe eines Koordinatensystems kann jedem Punkt P der Ebene eindeutig ein geordnetes Zahlenpaar – die Koordinaten dieses Punktes – zugeordnet werden. Die erste Koordinate (x-Koordinate, x-Wert oder Absizissi von P) gibt an, wie weit entfernt der Punkt P rechts oder links von der y-Achse liegt. Die zweite Koordinate (y-Koordinate, y-Wert oder Ordinate von P) sagt aus, wie weit P oberhalb oder unterhalb der x-Achse liegt. Umgekehrt gehört zu jedem Zahlenpaar (x; y) ein dadurch eindeutig bestimmter Punkt P der Ebene, der dann die Koordinaten x und y besitzt (interaktives Rechenbeispiel).

Durch jedes der oben beschriebenen Koordinatensysteme wird die Ebene in vier Quadranten geteilt. Es gilt für die Punkte

• des   I. Quadranten: x > 0 und y > 0,
• des  II. Quadranten: x < 0 und y > 0,
• des III. Quadranten: x < 0 und y < 0,
• des IV. Quadranten: x > 0 und y < 0.