Barometer
Barometer oder Druckmesser sind Geräte zur Messung des Luftdruckes und damit Druckmesser (Manometer) für einen speziellen Zweck. Sie unterscheiden sich von anderen Druckmessern im Wesentlichen nur durch den Messbereich, der um den normalen Luftdruck herum liegt.
Verbreitete Formen von Barometern sind Dosenbarometer und Quecksilberbarometer. Darüber hinaus gibt es weitere Bauformen, die meist nach den gleichen physikalischen Gesetzen arbeiten.
Barometer oder Druckmesser sind Geräte zur Messung des Luftdruckes und damit Druckmesser (Manometer) für einen speziellen Zweck. Der Name Barometer geht auf den französischen Mathematiker und Physiker BLAISE PASCAL zurück. Barometer unterscheiden sich von anderen Druckmessern im Wesentlichen nur durch den Messbereich, der um den normalen Luftdruck herum liegt. Dieser normale Luftdruck beträgt 1013 hPa. Da er in der Regel zwischen 970 hPa und 1030 hPa schwankt, wählt man als Messbereich für Barometer meist einen Bereich zwischen 960 und 1070 hPa. Das sind 960 bis 1070 Millibar (mbar) oder 720 bis 800 mm Quecksilbersäule (Torr).
Dosenbarometer
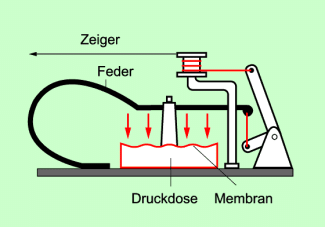
Ein Dosenbarometer, auch Federbarometer oder Aneroidbarometer genannt, dient zur Messung des Luftdrucks. Es besteht aus einer Metalldose (Druckdose) mit geringem Druck im Inneren. Diese Dose ist über eine Feder mit einem Hebelmechanismus verbunden. Der Mechanismus führt zu einem Zeiger, der sich vor einer Skala bewegen kann (Bild 2). Der Druck im Inneren der Dose, der Druck durch die Feder und der Luftdruck befinden sich im Gleichgewicht. Bei normalem Luftdruck wird der Zeiger auf den Wert 1 013 hPa (760 Torr) gestellt. Verändert sich nun der Luftdruck, so wird die Membran der Dose mehr oder weniger stark verformt. Über den Hebelmechanismus wird die Bewegung der Membran auf den Zeiger übertragen. An der Skala kann der jeweilige Wert des Luftdrucks abgelesen werden.
-
Aufbau eines Dosenbarometers
Quecksilberbarometer
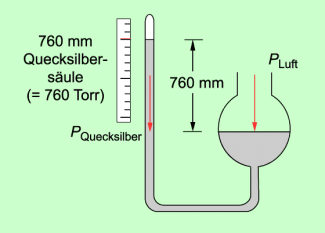
Ein Quecksilberbarometer besteht aus einem U-förmig gebogenen Glasrohr, in dem sich Quecksilber befindet (Bild 3). In dem einen (linken) Schenkel des Rohres wirkt der Druck des Quecksilbers, in dem anderen (rechten), nicht abgeschlossenen Rohr wirkt der Luftdruck. Gleichgewicht besteht dann, wenn beide Drücke gleich groß sind.
Sinkt der Luftdruck, dann sinkt auch die Höhe der Quecksilbersäule. Beim Steigen des Luftdruckes wird die Quecksilbersäule länger. Die Länge der Quecksilbersäule ist somit ein Maß für die Höhe des Luftdruckes. Bringt man eine Skala an, so kann man den Druck direkt in Millimeter Quecksilbersäule (Torr) oder auch in einer anderen Einheit ablesen.
-
Aufbau eines Quecksilberbarometers
Weitere Arten von Barometern
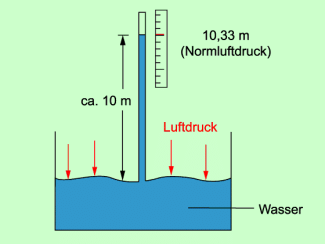
Verwendet man bei einem Barometer statt Quecksilber Wasser, dann erhält man ein Wasserbarometer (Bild 4). Ein solches Wasserbarometer ist im Prinzip genauso aufgebaut und funktioniert ebenso wie ein Quecksilberbarometer. Füllt man in einen einseitig geschlossenen durchsichtigen Schlauch oder in ein durchsichtiges Rohr Wasser und ordnet es so an, dass sich das offene Ende im Wasser befindet, dann ist im Gleichgewichtszustand der Druck der Wassersäule genau so groß wie der Luftdruck. Mit Veränderung des Luftdruckes verändert sich auch die Höhe der Wassersäule. Da aber die Dichte von Wasser wesentlich kleiner als die Dichte von Quecksilber ist, muss die Wassersäule wesentlich länger sein als die Quecksilbersäule, um dem Luftdruck das Gleichgewicht zuhalten. Es gilt:
760 mm Quecksilbersäule entsprechen 10,33 m Wassersäule.
Ein solches Wasserbarometer kann man sich aus durchsichtigem Schlauch selbst bauen.
Beachte: Erforderlich ist eine Höhe von mindestens 10 m.
-
Aufbau eines Wasserbarometers
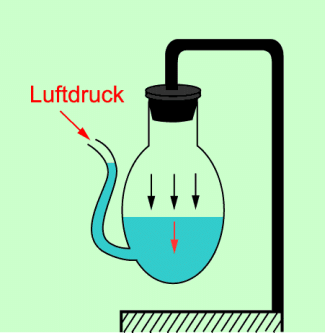
Eine weitere Bauform ist das GOETHE-Barometer, das der berühmte Dichter JOHANN WOLFGANG VON GOETHE (1749-1832) entwickelt haben soll (Bild 5). Es besteht aus einem geschlossenen Glasgefäß mit einem seitlichen Ansatz. Das Gefäß wird etwa halb mit angefärbtem Wasser gefüllt. Auf die Öffnung des seitlichen Ansatzes wirkt der Luftdruck. Er befindet sich im Gleichgewicht mit dem Druck der komprimierten Luft im geschlossenen Gefäß und den Drücken, die die beiden Wassersäulen ausüben. Vergrößert sich der Luftdruck, so sinkt die Wassersäule im seitlichen Ansatz.
-
Goethe-Barometer
Barograf
Eine besondere Bauform ist der Barograf. Er dient dazu, den Luftdruck kontinuierlich zu messen und die Messwerte aufzuzeichnen, so wie das für meteorologische Beobachtungen erforderlich ist. Ein Barograf ist meist genauso aufgebaut wie ein empfindliches Dosenbarometer. Statt des Zeigers wird ein Schreibstift befestigt, an dem sich eine mit Papier bespannte, von einem Uhrwerk angetriebene Trommel vorbeibewegt. Damit kann der Luftdruck ständig registriert werden.

